Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Đk: x >/ 1
Đặt \(\left\{{}\begin{matrix}a=\sqrt{3x-2}\\b=\sqrt{x-1}\end{matrix}\right.\left(a,b\ge0\right)\)
ta có hpt: \(\left\{{}\begin{matrix}a^2-3b^2=1\\a+b=3\end{matrix}\right.\)
Tự giải tiếp nhé, phương pháp thế. Chỉ cần ra được a HOẶC b thôi.
2) Đk: x >/ -1/4
Đặt \(\left\{{}\begin{matrix}a=\sqrt{4x+1}\\b=\sqrt{3x+4}\end{matrix}\right.\left(a,b\ge0\right)\)
ta có hpt: \(\left\{{}\begin{matrix}3a^2-4b^2=-13\\a-b=1\end{matrix}\right.\)
Tự làm tiếp nhé

ĐKXĐ: \(x\ge1\)
Do \(\sqrt{x-\sqrt{x^2-1}}.\sqrt{x+\sqrt{x^2-1}}=\sqrt{x^2-x^2+1}=1\)
Đặt \(\sqrt{x-\sqrt{x^2-1}}=t\Rightarrow\sqrt{x+\sqrt{x^2-1}}=\dfrac{1}{t}\)
Phương trình trở thành:
\(t+\dfrac{1}{t}=2\Rightarrow t^2-2t+1=0\Rightarrow t=1\)
\(\Rightarrow\sqrt{x-\sqrt{x^2-1}}=1\Leftrightarrow x-\sqrt{x^2-1}=1\)
\(\Leftrightarrow x-1=\sqrt{x^2-1}\)
\(\Rightarrow x^2-2x+1=x^2-1\)
\(\Rightarrow x=1\) (thỏa mãn)

Thích đặt ẩn phụ thì đặt vậy
Đặt \(\frac{1}{\sqrt{1-x^2}}=a\left(a>0\right)\) thì PT trở thành
\(a^2=3a-1\)
\(\Leftrightarrow\orbr{\begin{cases}a=\frac{3+\sqrt{5}}{2}\\a=\frac{3-\sqrt{5}}{2}\end{cases}}\)
Thế vô làm tiếp nhé
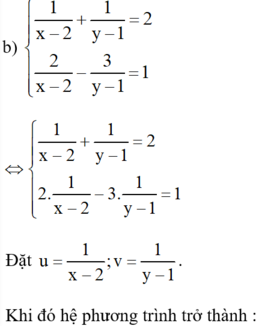
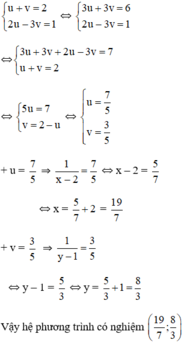
Đk: -3\<x\<2
Đặt \(\left\{{}\begin{matrix}a=\sqrt{3+x}\\b=\sqrt{2-x}\end{matrix}\right.\left(a,b\ge0\right)\)
Ta có hpt: \(\left\{{}\begin{matrix}a^2+b^2=5\left(1\right)\\a-b=1\left(2\right)\end{matrix}\right.\)
(2) \(a=1+b\) (*)
Thay (*) vào (1), ta được:
\(\left(1+b\right)^2+b^2=5\) \(\Leftrightarrow2b^2+2b-4=0\) \(\Leftrightarrow\left[{}\begin{matrix}b=1\left(N\right)\\b=-2\left(L\right)\end{matrix}\right.\)
Với b=1. ta có: \(\sqrt{2-x}=1\Leftrightarrow x=1\left(N\right)\)
Kl: x=1