Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{8}{\sqrt{5}-1}-\dfrac{22}{4+\sqrt{5}}+\dfrac{\sqrt{15}+2\sqrt{5}}{2+\sqrt{3}}\)
\(=\dfrac{8\left(\sqrt{5}+1\right)}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}-\dfrac{22\left(4-\sqrt{5}\right)}{\left(\sqrt{5}+4\right)\left(4-\sqrt{5}\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}+2\right)}{2+\sqrt{3}}\)
\(=\dfrac{8\sqrt{5}+8}{5-1}-\dfrac{88-22\sqrt{5}}{16-5}+\sqrt{5}\)
\(=\dfrac{8\sqrt{5}+8}{4}-\dfrac{88-22\sqrt{5}}{11}+\sqrt{5}\)
\(=2\sqrt{5}+2-8+2\sqrt{5}+\sqrt{5}=5\sqrt{5}-6\)

Ta có: \(\dfrac{\sqrt{8-2\sqrt{12}}}{\sqrt{3}-1}\)
\(=\dfrac{\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}}{\sqrt{3}-1}\)
\(=\sqrt{2}\)

a: ĐKXĐ: \(x>0\)
b: Ta có: \(A=\dfrac{x^2+\sqrt{x}}{x-\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+1\)
\(=x+\sqrt{x}-2\sqrt{x}-1+1\)
\(=x-\sqrt{x}\)

Ta có: \(\dfrac{1}{2+\sqrt{3}}+\sqrt{3}\)
\(=2-\sqrt{3}+\sqrt{3}\)
=2

Ta có: \(\dfrac{2\sqrt{3}}{\sqrt{3}+\sqrt{2}}+\sqrt{24}\)
\(=2\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)+2\sqrt{6}\)
\(=6-2\sqrt{6}+2\sqrt{6}\)
=6

\(B=\left(\dfrac{2x+1}{x\sqrt{x}-1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\right)\left(\dfrac{1+x\sqrt{x}}{1+\sqrt{x}}-\sqrt{x}\right)+\dfrac{2-2\sqrt{x}}{\sqrt{x}}(x \geq 0,x \neq 1\)
`=((2x+1-x+\sqrtx)/(x\sqrtx-1))(((\sqrtx+1)(x-\sqrtx+1))/(\sqrtx+1)-\sqrtx)+(2-2sqrtx)/sqrtx`
`=((x-\sqrtx+1)/((\sqrtx-1))(x+sqrtx+1)))(x-2\sqrtx+1)-(2\sqrtx-2)/sqrtx`
`=(1/(\sqrtx-1))(\sqrtx-1)^2-(2(\sqrtx-1))/sqrtx`
`=\sqrtx-1-(2(\sqrtx-1))/sqrtx`
`=(x-\sqrtx-2\sqrtx+2)/sqrtx`
`=(x-3sqrtx+2)/sqrtx`

\(=\left(\dfrac{x+3\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\right).\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{\left(x+2\sqrt{x}+1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}-3}{\sqrt{x}+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\)

a: \(=\dfrac{x-9-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{-5\sqrt{x}-5+x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-3\sqrt{x}-5}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}\)
b: khi x=6-2căn 5 thì \(P=\dfrac{6-2\sqrt{5}-3\sqrt{5}+3-5}{\left(\sqrt{5}-3\right)\left(\sqrt{5}-4\right)\cdot\sqrt{5}}\)
\(=\dfrac{-5\sqrt{5}+4}{\sqrt{5}\left(\sqrt{5}-3\right)\left(\sqrt{5}-4\right)}\)

a: \(C=\dfrac{3x+3\sqrt{x}-3-x+1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{\sqrt{x}}\cdot\dfrac{1-1+\sqrt{x}}{1-\sqrt{x}}\)
\(=\dfrac{2x+3\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-1-\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để \(C=\sqrt{x}\) thì \(x-\sqrt{x}=\sqrt{x}+1\)
=>\(x-2\sqrt{x}-1=0\)
=>\(\Leftrightarrow x=3+2\sqrt{2}\)
c: |2x-5|=3
=>2x-5=3 hoặc 2x-5=-3
=>2x=2 hoặc 2x=8
=>x=4(nhận) hoặc x=1(loại)
Khi x=4 thì \(C=\dfrac{2+1}{2-1}=3\)
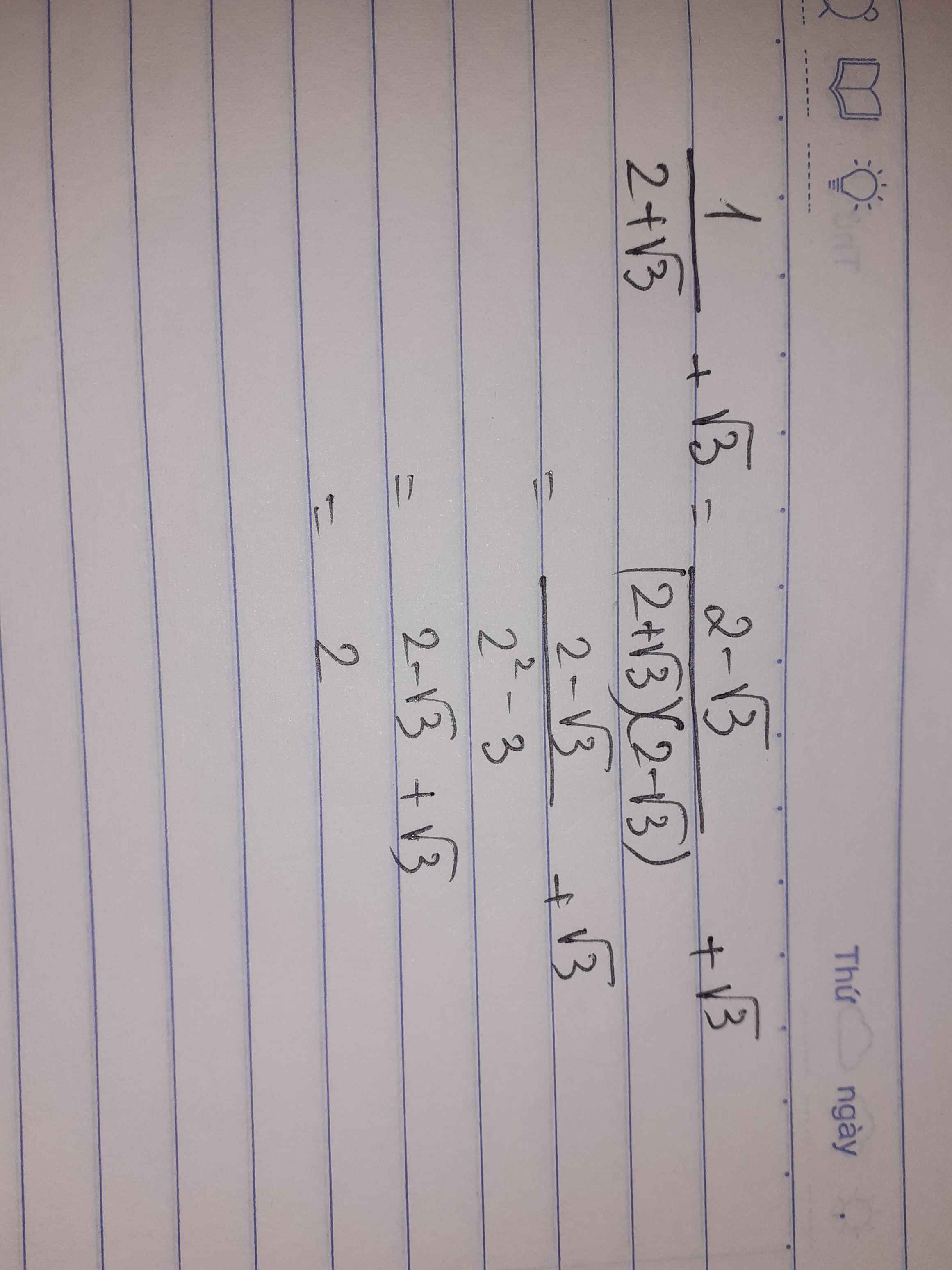
\(\sqrt{3+2\sqrt{2}}-\sqrt{\dfrac{\sqrt{2}-1}{\sqrt{2}+1}}\)
\(=\sqrt{2+2\sqrt{2}+1}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}\right)^2+2\sqrt{2}\cdot1+1^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}+1\right)\left(\sqrt{2}-1\right)}}\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{\left(\sqrt{2}\right)^2-1^2}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{2-1}}\)
\(=\sqrt{2}+1-\sqrt{\dfrac{\left(\sqrt{2}-1\right)^2}{1}}\)
\(=\sqrt{2}+1-\sqrt{\left(\sqrt{2}-1\right)^2}\)
\(=\sqrt{2}+1-\left(\sqrt{2}-1\right)\)
\(=\sqrt{2}+1-\sqrt{2}+1=2\)