
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



THAM KHẢO
Gọi x là v.tốc dự định của xe(x>0, km/h)
Nửa quãng đường xe đi là: 120:2=60(km)
=> Vận tốc đi nửa quãng đường là: 60x60x (km/h)
=> Thời gian đi dự định là: 120x(h)120x(h)
Vì nửa qquangx đường sau xe đi với thời gian là: 60x+10(h)60x+10(h)
Theo bra ta có:
60x+60x+10=120x−0.560x+60x+10=120x−0.5
Gải được x=40(tmđk)
Vậy v.tốc dự định là 40km/h

a) \(A=4x-x^2+3\)
\(\Leftrightarrow A=-\left(x^2-4x+4\right)+7\)
\(\Leftrightarrow A=-\left(x-2\right)^2+7\le7,\forall x\in R\)
\(\Rightarrow GTLN\left(A\right)=7\left(tại.x=2\right)\)
b) \(B=-3x^2+5x+2\)
\(\Leftrightarrow B=-3\left(x^2-\dfrac{5}{3}x+\dfrac{25}{36}\right)+\dfrac{25}{12}+2\)
\(\Leftrightarrow B=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{49}{12}\le\dfrac{49}{12},\forall x\in R\)
\(\Rightarrow GTLN\left(B\right)=\dfrac{49}{12}\left(tại.x=\dfrac{5}{6}\right)\)
\(a,A=4x-x^2+3\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7\)
Ta có: \(\left(x-2\right)^2\ge0\forall x\)
\(\Rightarrow-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2+7\le7\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow-\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\Leftrightarrow x=2\)
Vậy \(Max_A=7\) khi \(x=2\)
\(b,B=-3x^2+5x+2\)
\(=-3x^2+5x-\dfrac{25}{12}+\dfrac{25}{12}+2\)
\(=-3\left(x^2-\dfrac{5}{3}x+\dfrac{25}{36}\right)+\dfrac{49}{12}\)
\(=-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{49}{12}\)
Ta có: \(\left(x-\dfrac{5}{6}\right)^2\ge0\forall x\)
\(\Rightarrow-3\left(x-\dfrac{5}{6}\right)^2\le0\forall x\)
\(\Rightarrow-3\left(x-\dfrac{5}{6}\right)^2+\dfrac{49}{12}\le\dfrac{49}{12}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow-3\left(x-\dfrac{5}{6}\right)^2=0\)
\(\Leftrightarrow x-\dfrac{5}{6}=0\Leftrightarrow x=\dfrac{5}{6}\)
Vậy \(Max_B=\dfrac{49}{12}\) khi \(x=\dfrac{5}{6}\)
#Toru


1) \(x^3-8x+7=\left(x-1\right)\left(x^2+x-7\right)\)
2) \(x^3+8x^2-9=\left(x-1\right)\left(x^2+9x+9\right)\)
3) \(3x^3-4x+1=\left(x-1\right)\left(3x^2+3x-1\right)\)
4) \(x^4-3x^2+3x-1=\left(x-1\right)\left(x^3+x^2-2x+1\right)\)
5) \(x^4-5x^2+4=\left(x-1\right)\left(x-2\right)\left(x+1\right)\left(x+2\right)\)
1: Ta có: \(x^3-8x+7\)
\(=x^3-x-7x+7\)
\(=x\left(x-1\right)\left(x+1\right)-7\left(x-1\right)\)
\(=\left(x-1\right)\left(x^2+x-7\right)\)
2: Ta có: \(x^3+8x^2-9\)
\(=x^3-x^2+9x^2-9\)
\(=x^2\left(x-1\right)+9\left(x-1\right)\left(x+1\right)\)
\(=\left(x-1\right)\left(x^2+9x+9\right)\)
3: Ta có: \(3x^3-4x+1\)
\(=3x^3-3x-x+1\)
\(=3x\left(x-1\right)\left(x+1\right)-\left(x-1\right)\)
\(=\left(x-1\right)\left(3x^2+3x-1\right)\)
4: Ta có: \(x^4-3x^2+3x-1\)
\(=\left(x-1\right)\left(x+1\right)\left(x^2+1\right)-3x\cdot\left(x-1\right)\)
\(=\left(x-1\right)\cdot\left(x^3+x+x^2+1-3x\right)\)
\(=\left(x-1\right)\left(x^3+x^2-2x+1\right)\)


Câu 2:
\(\Leftrightarrow\left(x+2\right)\left(10x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-\dfrac{3}{10}\end{matrix}\right.\)
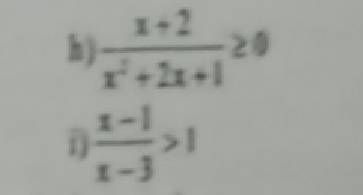
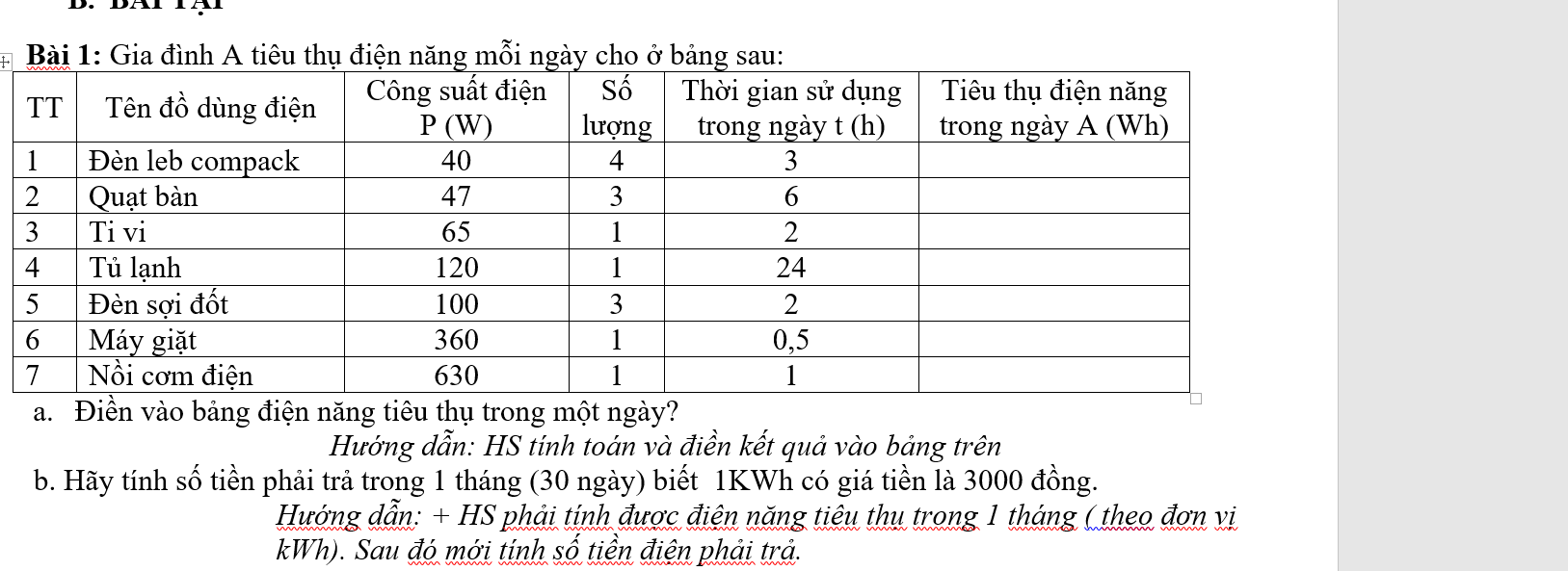



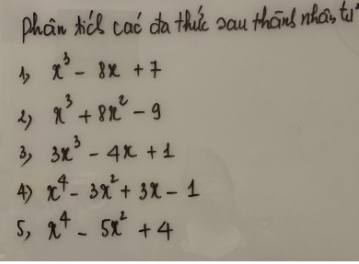



h)\(\dfrac{x+2}{x^2+2x+1}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)^2}\ge0\)
⇔\(\dfrac{x+2}{\left(x+1\right)\left(x+1\right)}\ge\dfrac{0.\left(x+1\right)\left(x+1\right)}{\left(x+1\right)\left(x+1\right)}\)
⇒\(x+2\ge0\)
⇔\(x+2-2\ge0-2\)
⇔\(x\ge-2\)
i)\(\dfrac{x-1}{x-3}>1\)
⇔\(\dfrac{x-1}{x-3}>\dfrac{1.\left(x-3\right)}{1.x-3}\)
⇒\(x-1>x-3\)
⇔\(x-x>-3+1\)
⇔\(0x>-2\)