Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 199010+19909 là A
Gọi 199110 là B
A=199010+19909=19909(1990+1)=19909.1991
B=199110=19919.1991
Vậy A<B

a) \(2^x=16=2^4\Rightarrow x=4\)
b) \(x^3=27=3^3\Rightarrow x=3\)
c) \(x^{50}=x\Rightarrow x\left(x^{49}-1\right)=0\Rightarrow x=0\) hay \(x=1\)
d) \(\left(x-2\right)^2=16=4^2\Rightarrow x-2=4\) hay \(x-2=-4\)
\(\Rightarrow x=6\) hay \(x=-2\)
a) \(2^{300}=2^{3.100}=8^{100}\)
\(3^{200}=3^{2.100}=9^{100}\)
vì \(8^{100}< 9^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(3^{500}=3^{5.100}=243^{100}\)
\(7^{300}=7^{3.100}=343^{100}\)
vì \(243^{100}< 343^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)

`3^(2 + n) và 2^(3 + n) `
`3^(2 + n) = 3^2 xx 3^n = 9 xx 3^n`
`2^(3 + n) = 2^3 xx 2^n = 8 xx 2^n`
ta thấy `9>8 ; 3^n > 2^n `
vậy `3^(2 + n) > 2^(3 + n) `

202³⁰³ = (202³)¹⁰¹ = 8242408¹⁰¹
303²⁰² = (303²)¹⁰¹ = 91809¹⁰¹
Do 8242408 > 91809 nên 8282408¹⁰¹ > 91809¹⁰¹
Vậy 202³⁰³ > 303²⁰²

a) 3^2 và 3.2
3^2=9
3.2=6
-> 3^2>3.2
b)2^3 và 3^2
2^3=8
3^2=9
-> 2^3<3^2
c) 3^3 và 3^4
Vì hai số có cùng cơ số nên ta so sánh số mũ
3<4
-> 3^3<3^4
a)ta có 32=9 ; 3.2=6 => 32 > 3.2
b)ta có 23=8 ; 32=9 => 23 < 32
c) ta có 33 và 34
vì 2 số đều cùng 1 cơ số
mà cơ số đầu có số mũ = 3,cơ số còn lại có lũy thừa =4
=> 3<4
=> 33<34

a) \(243^5=\left(3^5\right)^5=3^{25}\)
\(3\cdot27^5=3\cdot\left(3^3\right)^5=3\cdot3^{15}=3^{16}\)
mà \(3^{25}>3^{16}\)
nên \(243^5>3\cdot27^5\)
b) \(625^5=\left(5^4\right)^5=5^{20}\)
\(125^7=\left(5^3\right)^7=5^{21}\)
mà \(5^{20}< 5^{21}\)
nên \(625^5< 125^7\)
c) \(202^{303}=\left(202^3\right)^{101}=8242408^{101}\)
\(303^{202}=\left(303^2\right)^{101}=91809^{101}\)
mà \(8242408^{101}>91809^{101}\)
nên \(202^{303}>303^{202}\)
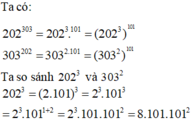
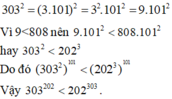

a) 31^11<32^11=2^55<2^56=(2^4)^14=16^14<17^14
b) 5^2n=25^n<32^n=2^5n
c) 3^500=(3^5)^100=243^100
7^300=(7^3)^100=343^100
Có 243^100<343^100 nên 3^500<7^300
d)8^5=2^15=2^14.2
3.4^7=3.2^14
Có 2.2^14<3.2^14 nên 8^5<3.4^7
------------------Hok tốt------------------
a, Ta có :
3111 < 3211 = ( 25 )11 = 255 ( 1 )
1714 > 1614 = ( 24 )14 = 256 ( 2 )
Từ 1 và 2 => 3111 < 1714