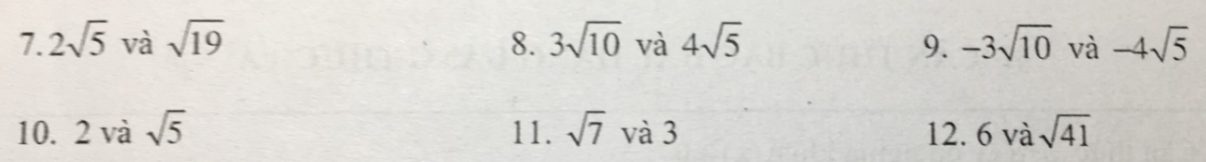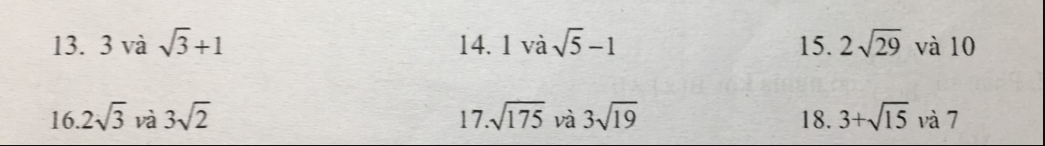Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:
\(2=1+1=1+\sqrt{1}\)
Mà: \(1< 2\Rightarrow\sqrt{1}< \sqrt{2}\)
\(\Rightarrow1+\sqrt{1}< \sqrt{2}+1\)
\(\Rightarrow2< \sqrt{2}+1\)
b) Ta có:
\(1=2-1=\sqrt{4}-1\)
Mà: \(4>3\Rightarrow\sqrt{4}>\sqrt{3}\)
\(\Rightarrow\sqrt{4}-1>\sqrt{3}-1\)
\(\Rightarrow1>\sqrt{3}-1\)
c) Ta có:
\(10=2\cdot5=2\sqrt{25}\)
Mà: \(25< 31\Rightarrow\sqrt{25}< \sqrt{31}\)
\(\Rightarrow2\sqrt{25}< 2\sqrt{31}\)
\(\Rightarrow10< 2\sqrt{31}\)
d) Ta có:
\(-12=-3\cdot4=-3\sqrt{16}\)
Mà: \(16>11\Rightarrow\sqrt{16}>\sqrt{11}\)
\(\Rightarrow-3\sqrt{16}< -3\sqrt{11}\)
\(\Rightarrow-12< -3\sqrt{11}\)

7: \(2\sqrt{5}=\sqrt{20}>\sqrt{19}\)
8: \(3\sqrt{10}=\sqrt{90}>\sqrt{80}=4\sqrt{5}\)
9: \(3\sqrt{10}>4\sqrt{5}\)
nên \(-3\sqrt{10}< -4\sqrt{5}\)
10: \(2=\sqrt{4}< \sqrt{5}\)
11: \(\sqrt{7}< \sqrt{9}=3\)
12: \(6=\sqrt{36}< \sqrt{41}\)
\(2\sqrt{5}>\sqrt{19};3\sqrt{10}>4\sqrt{5};-3\sqrt{10}< 4\sqrt{5}\)
\(2< \sqrt{5};\sqrt{7}< 3;6< \sqrt{41}\)

\(3>\sqrt{3}+1;1< \sqrt{5}-1;2\sqrt{29}>10\)
\(2\sqrt{3}>3\sqrt{2};\sqrt{175}>3\sqrt{19};3+\sqrt{15}< 7\)

Lời giải:
\(\frac{1}{\sqrt{7}}+\frac{1}{\sqrt{11}}> \frac{1}{\sqrt{4}}+\frac{1}{\sqrt{9}}=\frac{5}{6}>\frac{4}{6}=\frac{2}{3}\)

Bài 1. Tính căn bậc hai số học của các số sau:
1) 36=\(\sqrt{36}=4\)
2) 81\(\sqrt{81}=9\)
3) 121=\(\sqrt{121}=11\)
4) 144=\(\sqrt{144}=12\)
5) 0,16=\(\sqrt{0,16}=0,4\)
7) 29=\(\sqrt{29}~5,39\)
8) 0=\(\sqrt{0}=0\)
Bài 2:
1: \(\sqrt{6}< \sqrt{41}\)
2: \(\sqrt{19}>\sqrt{4}\)
3: \(\sqrt{21}>\sqrt{5}\)
4: \(\sqrt{7}< \sqrt{51}\)

5 x 2 + 20 = 0 ⇔ 5 x 2 = - 20
Vế trái 5 x 2 ≥ 0; vế phải -20 < 0
Không có giá trị nào của x để 5 x 2 = - 20
Phương trình vô nghiệm.
∆ = 0 2 - 4.5.20 = - 400 < 0. Phương trình vô nghiệm.