
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 18 2 < 10 3
b) 3 2 + 4 2 < ( 3 + 4 ) 2
c) 100 2 + 30 2 < ( 100 + 30 ) 2
d) a 2 + b 2 > ( a - b ) 2 với a ∈ N * ; b ∈ N * .

Bài 1
a) S = 1 + 2 + 2² + 2³ + ... + 2²⁰²³
2S = 2 + 2² + 2³ + 2⁴ + ... + 2²⁰²⁴
S = 2S - S = (2 + 2² + 2³ + ... + 2²⁰²⁴) - (1 + 2 + 2² + 2³)
= 2²⁰²⁴ - 1
b) B = 2²⁰²⁴
B - 1 = 2²⁰²⁴ - 1 = S
B = S + 1
Vậy B > S
a,
\(S=1+2+2^2+...+2^{2023}\)
\(2S=2+2^2+2^3+...+2^{2024}\)
\(\Rightarrow S=2^{2024}-1\)
b.
Do \(2^{2024}-1< 2^{2024}\)
\(\Rightarrow S< B\)
2.
\(H=3+3^2+...+3^{2022}\)
\(\Rightarrow3H=3^2+3^3+...+3^{2023}\)
\(\Rightarrow3H-H=3^{2023}-3\)
\(\Rightarrow2H=3^{2023}-3\)
\(\Rightarrow H=\dfrac{3^{2023}-3}{2}\)

\(32^{15}=\left(2^5\right)^{15}=2^{5.15}=2^{75}\)
\(4^{39}=\left(2^2\right)^{39}=2^{2.39}=2^{78}\)
Do \(2^{78}>2^{75}\)
\(\Rightarrow4^{39}>32^{15}\)
\(\Rightarrow1+4+4^2+...+4^{39}>32^{15}\)
\(\Rightarrow3\left(1+4+4^2+...+4^{39}\right)>32^{15}\)
Vậy \(A>B\)



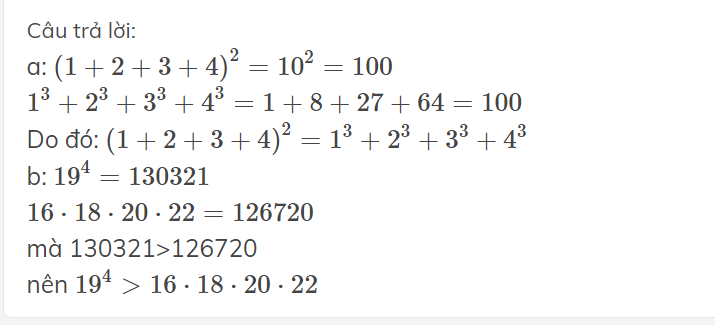
ta có:
\(a=\frac{1}{2^2}+\frac{1}{3^2}+...+\frac{1}{100^2}\)
\(a=\frac{1}{4}+\frac{1}{9}+...+\frac{1}{9801}+\frac{1}{10000}\)
\(a=\left(\frac{1}{4}+\frac{1}{10000}\right)+\left(\frac{1}{9}+\frac{1}{9801}\right).\left(10000-4:\left(9-4\right)\right)\)
a=\(\frac{1}{10004}.498=\frac{249}{5002}\)
vì:\(\frac{249}{5002}< \frac{3}{4}=>a< \frac{3}{4}\)