K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
16 tháng 10 2019
Ta có: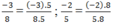 
Vì (-3).5 > 8 . (-2) nên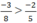 
Với hai phân số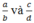 
(a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu 
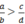thì ad > bc hoặc 
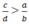thì cb > ad
Ta chứng minh: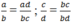 
Ta có: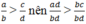 
Theo quy tắc so sánh hai phân số ta có: ad > bc
Theo chiều ngược lại, ta cũng có:
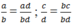
Theo quy tắc so sánh hai phân số nếu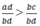 
Suy ra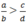 
27 tháng 9 2021
a: \(A=2019\cdot2021=2020^2-1\)
\(B=2020^2\)
Do đó: A<B
HN
10 tháng 10 2021
Fhzhizuu8zìtcùbìgìvìg⁸fu7fdjhtvfghhhujfghfhgkffztdhcvvgoh. Gtvguvvhhvhvzcgctv
DX
1
TT
3 tháng 2 2021
a/ \(2^{225}=\left(2^3\right)^{75}=8^{75}\)
\(3^{151}>3^{150}=\left(3^2\right)^{75}=9^{75}\)
Mà \(8^{75}< 9^{75}\)
=> \(2^{225}< 3^{150}< 3^{151}\)
b/ Xét n là số lẻ
=> n + 1 chẵn
=> n + 1 ⋮ 2
=> (n+1)(3n+2) ⋮2
Xét n là số chẵn
=> 3n chẵn
=> 3n+2 chẵn
=> (n+1)(3n+2) ⋮2
Do đó A = (n+1)(3n+2) chia hết cho 2 với mọi số tự nhiên n
F
0
KK
21 tháng 7 2019
Chị ngại đánh máy nên ns cách lm thôi nhé
A) E nhân C vs 2 thì sẽ xuất hiện 2^90
Sau đó lấy 2C - C thì sẽ triệt tiêu hết còn 2^90 - 1 hay C = 2^90 -1 => C<2^90
B) 1 + 2 + 2^2 =7
=> Nhóm C thành các nhóm sao có chứ 1 + 2 + 2^2 ( lưu ý là mấy nhóm sau phải đặt một lũy thừa của 2 ra ngoài mới xuất hiện đc tổng đó nhé )
C) 1 + 2 + 2^2 + 2^3 = 15
Em nhóm ra như cách làm phần B thì được 22 nhóm, dư 2 số cuối => C ko chia hết cho 15
Ko hiểu chỗ nào thì hỏi nhé
F
21 tháng 7 2019
Bài giải
Ta có :
a, \(C=1+2+2^2+...+2^{89}\)
\(2C=2+2^2+2^3+....+2^{90}\)
\(2C-C=2^{90}-1\)
\(\Rightarrow\text{ }C=2^{90}-1\)
b, \(C=1+2+2^2+...+2^{89}\)
\(C=1+2+2^2+\left(2^3+2^4+2^5\right)+...+\left(2^{87}+2^{88}+2^{89}\right)\)
\(C=1+2+2^2+2^3\left(1+2+2^2\right)+...+2^{87}\left(1+1+2^2\right)\)
\(C=7+2^3\cdot7+...+2^{87}\cdot7\)
\(\Rightarrow\text{ }C\text{ }⋮\text{ }7\)
c, Bạn làm tương tự câu b nha !
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 8 2023
Bài 1:
\(2^{49}=\left(2^7\right)^7=128^7;5^{21}=\left(5^3\right)^7=125^7\\ Vì:128^7>125^7\Rightarrow2^{49}>5^{21}\)
Bài 2:
\(a,S=1+3+3^2+3^3+...+3^{99}\\ =\left(1+3+3^2+3^3\right)+3^4.\left(1+3+3^2+3^3\right)+...+3^{96}.\left(1+3+3^2+3^3\right)\\ =40+3^4.40+...+3^{96}.40\\ =40.\left(1+3^4+...+3^{96}\right)⋮40\\ b,S=1+4+4^2+4^3+...+4^{62}\\ =\left(1+4+4^2\right)+4^3.\left(1+4+4^2\right)+...+4^{60}.\left(1+4+4^2\right)\\ =21+4^3.21+...+4^{60}.21\\ =21.\left(1+4^3+...+4^{60}\right)⋮21\)
1 tháng 8 2023
Bài 1 :
\(2^{49}=\left(2^7\right)^7=128^7\)
\(5^{21}=\left(5^3\right)^7=125^7\)
mà \(125^7< 128^7\)
\(\Rightarrow2^{49}>5^{21}\)
Bài 2 :
a) \(S=1+3+3^2+3^3+...3^{99}\)
\(\Rightarrow S=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)...+3^{96}\left(1+3+3^2+3^3\right)\)
\(\Rightarrow S=40+40.3^4+...+40.3^{96}\)
\(\Rightarrow S=40\left(1+3^4+...+3^{96}\right)⋮40\)
\(\Rightarrow dpcm\)
b) \(S=1+4+4^2+4^3+...4^{62}\)
\(\Rightarrow S=\left(1+4+4^2\right)+4^3\left(1+4+4^2\right)+...4^{60}\left(1+4+4^2\right)\)
\(\Rightarrow S=21+4^3.21+...4^{60}.21\)
\(\Rightarrow S=21\left(1+4^3+...4^{60}\right)⋮21\)
\(\Rightarrow dpcm\)