
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


2300 = (23)100 = 8100 và 3200 = (32)100 = 9100 nên 2300 < 3200;

a) \(2^{300}=\left(2^3\right)^{100}=8^{100}\)
\(3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}\)
\(\Rightarrow2^{300}< 3^{200}\)
b) \(99^{20}=\left(99^2\right)^{10}=9801^{10}< 9999^{10}\Rightarrow99^{20}< 9999^{10}\)
c) \(3^{500}=\left(3^5\right)^{100}=243^{100}\)
\(7^{300}=\left(7^3\right)^{100}=343^{100}>243^{100}\)
\(\Rightarrow3^{500}< 7^{300}\)

so sánh
a) 3200và 2300
Ta có :
2300 = (23)100 = 8100
3200 = ( 32)100 = 9100
2300 < 3200
b) 912 và 268
Ta có :
912 = ( 93)4 = 7294
268 = ( 262)4 = 6764
912>268
a, Ta có:
\(3^{200}\) = \(\left(3^2\right)^{100}\) = \(9^{100}\)
\(2^{300}\) = \(\left(2^3\right)^{100}\)= \(8^{100}\)
Vì 8 < 9 => \(8^{100}\) < \(9^{100}\)
Hay \(3^{200}\) < \(2^{300}\)
b, Ta có:
\(9^{12}\) = \(\left(9^3\right)^4\) = \(729^4\)
\(26^8\) = \(\left(26^2\right)^4\) = \(676^4\)
Vì 729 > 676 => \(729^4\) < \(676^4\)
Hay \(9^{12}\) < \(26^8\)

Khó vãi!!! Nghỉ ở nhà bây giờ ko nhớ tí kiến thức gì lun!!! Chắc phải mơ sách giáo khoa ra rùi tự nghiên cứu lại thui!!!

a) 1030 và 2100 .
1030 = ( 103 )10 = 100010 .
2100 = ( 210 )10 = 102410 .
Vì 100010 < 102410 .
\(\Rightarrow\) 1030 < 2100 .
Vậy ....
b) \(\uparrow\) Lm như trên .

-315/380 = -120015/144780
-316/381 = -120080/144780
Do -120015 > -120080
-120015/144780 > -120080/144780
⇒ -315/380 > -316/381
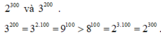
+)\(8^2=\left(2^3\right)^2=2^6\)
+)\(3^{200}=3^{2.100}=\left(3^2\right)^{100}=9^{100}\)
\(2^{300}=2^{3.100}=\left(2^3\right)^{100}=8^{100}\)
Vì \(9>8\Rightarrow9^{100}>8^{100}\)hay \(3^{200}>2^{300}\)
+)\(9^{20}=\left(3^2\right)^{20}=3^{40}\)
\(27^{13}=\left(3^3\right)^{13}=3^{39}\)
Vì \(40>39\Rightarrow3^{40}>3^{39}\)hay \(9^{20}>27^{13}\)
+)\(10^{20}=10^{2.10}=\left(10^2\right)^{10}=100^{10}\)
\(2^{100}=2^{10.10}=\left(2^{10}\right)^{10}=1024^{10}\)
Vì \(100< 1024\Rightarrow100^{10}< 1024^{10}\)hay \(10^{20}< 2^{100}\)
+)\(2^{161}=2^{4.40+1}=\left(2^4\right)^{40}.2=16^{40}.2\)
Vì \(13< 16\Rightarrow13^{40}< 16^{40}\)\(\Rightarrow13^{40}< 2^{161}\)