WK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 4 2017
Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
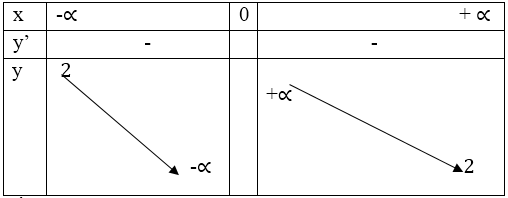
- Bảng biến thiên:
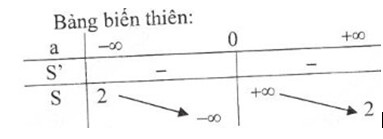
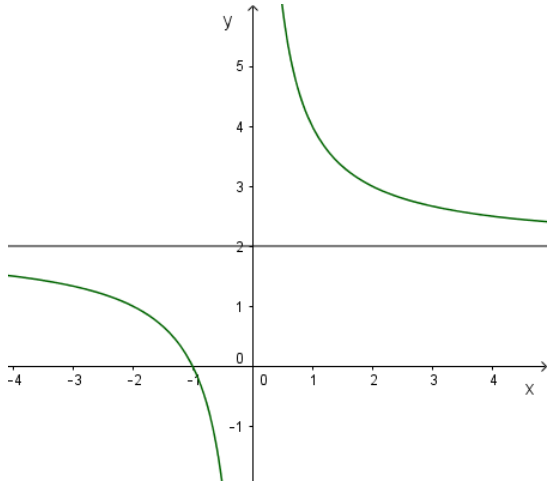
Đồ thị hàm số:
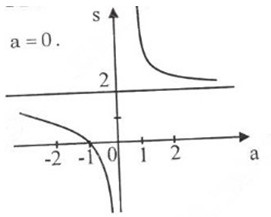
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
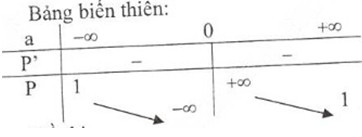
Đồ thị hàm số:
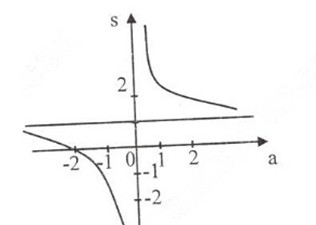
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.
TA
5 tháng 4 2016
Điều kiện :
\(\begin{cases}x-2>0\\3x-5>0\end{cases}\) \(\Leftrightarrow x>2\)
Phương trình tương đương \(\log_2\left(x-2\right)+\log_2\left(3x-5\right)=2\)
\(\Leftrightarrow\log_2\left[\left(x-2\right)\left(3x-5\right)\right]=2\Leftrightarrow3x^2-11x+6=0\)
Giải phương trình trên và đối chiếu với điều kiện ta được nghiệm phương trình đã cho là x=3
Đặt \(3^x=t>0\Rightarrow t^2-2\left(7-x\right)t+45-18x=0\)
\(\Delta'=\left(7-x\right)^2-\left(45-18x\right)=\left(x+2\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}t=7-x+x+2=9\\t=7-x-\left(x+2\right)=5-2x\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3^x=9\Rightarrow x=2\\3^x=5-2x\left(1\right)\end{matrix}\right.\)
Xét (1) \(\Leftrightarrow3^x+2x-5=0\)
Nhận thấy \(x=1\) là 1 nghiệm của (1)
Xét hàm \(f\left(x\right)=3^x+2x-5\Rightarrow f'\left(x\right)=3^x.ln3+2>0;\forall x\)
\(\Rightarrow f\left(x\right)\) đồng biến trên R nên \(f\left(x\right)\) có tối đa 1 nghiệm
\(\Rightarrow x=1\) là nghiệm duy nhất của (1)
Vậy pt đã cho có 2 nghiệm thực \(x=\left\{1;2\right\}\)