Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Cách giải:
![]()
![]()
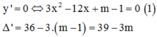
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 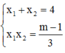
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
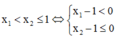
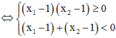
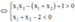
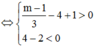 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006

ĐK: x#1
Ta có
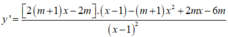
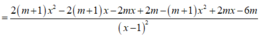
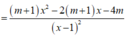
Để hàm số đồng biến trên 4 ; + ∞ thì y ' ≥ 0 ; ∀ x > 4
![]()
![]()
+ Với m+1=0 ⇔ m=-1 ⇒ 0>-4 (luôn đúng) nên nhận m=-1.(1)
+ Với m+1>0
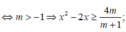
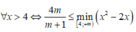
Xét hàm số g ( x ) = x 2 - 2 x có g ' ( x ) = 2 x - 2 = 0 ⇔ x = 1 ∉ 4 ; + ∞ , ta có BBT trên 4 ; + ∞ là
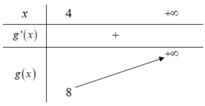
Từ BBT suy ra
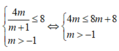
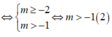
+ Với m+1<0 ⇔ m < - 1
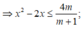
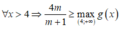
Từ BBT của g(x) suy ra không có m thỏa mãn.
Từ (1) và (2) suy ra m ≥ - 1 mà m ∈ - 2019 ; 2019 và m nguyên nên m ∈ - 1 ; 0 ; . . ; 2019 ⇒ có 2021 số thỏa mãn.
Chọn đáp án D.

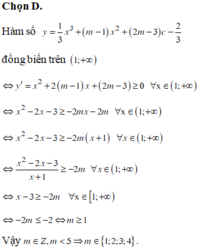


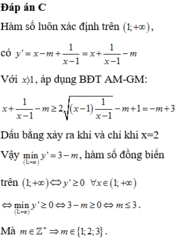
Đáp án D