K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
6 tháng 11 2017
Đáp án D
Cách giải:
![]()
![]()
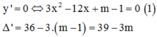
+ ![]() => Hàm số đồng biến trên
=> Hàm số đồng biến trên ![]()
+ ![]() Phương trình (1) có 2 nghiệm phân biệt
Phương trình (1) có 2 nghiệm phân biệt ![]()
Theo đinh lí Viet ta có 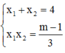
Khi đó, để hàm số đồng biến trên khoảng (1;+∞) thì
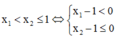
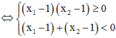
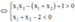
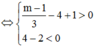 ( vô lí )
( vô lí )
Vậy m ≥ 13
Mà ![]()
![]()
Số giá trị của m thỏa mãn là: 2018 - 13 + 1 = 2006
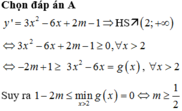

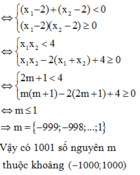
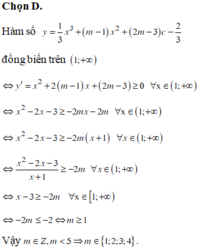

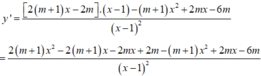
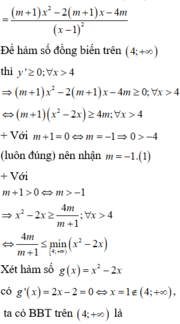
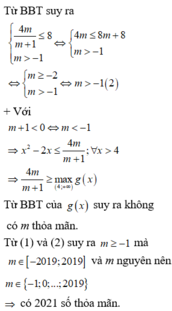


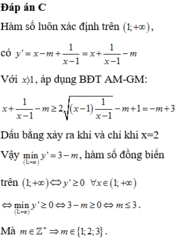
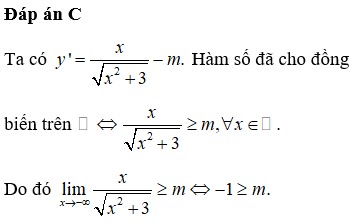
ĐK: x#1
Ta có
Để hàm số đồng biến trên 4 ; + ∞ thì y ' ≥ 0 ; ∀ x > 4
+ Với m+1=0 ⇔ m=-1 ⇒ 0>-4 (luôn đúng) nên nhận m=-1.(1)
+ Với m+1>0
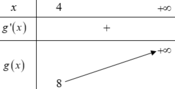
Xét hàm số g ( x ) = x 2 - 2 x có g ' ( x ) = 2 x - 2 = 0 ⇔ x = 1 ∉ 4 ; + ∞ , ta có BBT trên 4 ; + ∞ là
Từ BBT suy ra
+ Với m+1<0 ⇔ m < - 1
Từ BBT của g(x) suy ra không có m thỏa mãn.
Từ (1) và (2) suy ra m ≥ - 1 mà m ∈ - 2019 ; 2019 và m nguyên nên m ∈ - 1 ; 0 ; . . ; 2019 ⇒ có 2021 số thỏa mãn.
Chọn đáp án D.