Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \({u_9} = {u_1}.{q^{9 - 1}} = \left( { - 5} \right){.2^8} = - 1280\)
b) Ta có: \( - 320 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = 64 \Leftrightarrow n = 7\)
\( - 320\) là số hạng thứ 7 của cấp số nhân
c) Ta có: \(160 = \left( { - 5} \right){.2^{n - 1}} \Leftrightarrow {2^{n - 1}} = - {2^5}\)
160 không là số hạng của cấp số nhân

Kí hiệu u1,u2,u3,u4,u5 là các số hạng của cấp số nhân
Ta có :
![]()
![]()
![]()
![]()
![]()
![]()
Đáp án C

a) Cấp số nhân có \({u_1} = 1,\;\;q = \;4\)
Số hạng tổng quát: \({u_n} = {4^{n - 1}}\)
Số hạng thứ 5: \({u_5} = {4^{5 - 1}} = 256\)
Số hạng thứ 100: \({u_{100}} = {4^{100 - 1}} = {4^{99}}\).
b) Cấp số nhân có \({u_1} = 2,\;q = - \frac{1}{4}\)
Số hạng tổng quát: \({u_n} = 2 \times {\left( { - \frac{1}{4}} \right)^{n - 1}}\)
Số hạng thứ 5: \({u_5} = 2 \times {\left( { - \frac{1}{4}} \right)^{5 - 1}} = \frac{1}{{128}}\)
Số hạng thứ 100: \({u_{100}} = 2 \times {\left( { - \frac{1}{4}} \right)^{100 - 1}} = \frac{ -1}{{2^{197}}}\)

Phương pháp:
Số hạng tổng quát của CSN : u n = u 1 . q n - 1
Cách giải:
Ta có: u 1 = 2 , q = 3
![]()
Chọn D

Nếu cấp số nhân có công bội q = 1 thì cấp số nhân là \(u_1, u_1, ..., u_1,...\) Khi đó
\({S_n} = u_1 + u_1 + ... + u_1 = n . u_1\) (tổng của n số hạng u_1).

\(u_2=u_1+d=-2+d\) ; \(v_2=v_1q=-2q\)
\(u_2=v_2\Rightarrow-2+d=-2q\Rightarrow d=2-2q\)
\(u_3=v_3+8\Leftrightarrow-2+2d=-2q^2+8\)
\(\Leftrightarrow-2+2\left(2-2q\right)=-2q^2+8\)
\(\Leftrightarrow2q^2-4q-6=0\Rightarrow\left[{}\begin{matrix}q=-1\Rightarrow d=4\\q=3\Rightarrow d=-4\end{matrix}\right.\)
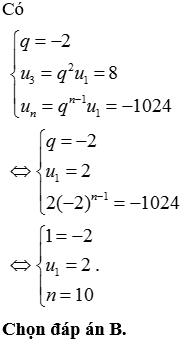
Phương pháp:
Cấp số nhân ( u n ) có số hạng đầu u 1 và công bội q thì có số hạng thứ n là
Cách giải:
Gọi số hạng thứ n là u n = 1458
⇔ 2 . 3 n - 1 = 1458
⇔ 3 n - 1 = 729 ⇔ n - 1 = 6 ⇔ n = 7
Chọn: D