T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
VT
3
21 tháng 10 2021
Bài 3:
\(a,=3x\left(y-4x+6y^2\right)\\ b,=5xy\left(x^2-6x+9\right)=5xy\left(x-3\right)^2\\ d,=\left(x+y\right)\left(x-12\right)\\ f,=2x\left(x-y\right)\left(5x-4y\right)\\ g,=\left(x-2\right)\left(x-2+3x\right)=\left(x-2\right)\left(4x-2\right)=2\left(x-2\right)\left(2x-1\right)\\ h,=x^2\left(1-5x\right)+3xy\left(5x-1\right)=x\left(1-5x\right)\left(x-3y\right)\\ i,=x\left(x-2\right)+4\left(x-2\right)=\left(x+4\right)\left(x-2\right)\\ j,=x^2-2x-3x+6=\left(x-2\right)\left(x-3\right)\\ k,=4x^2-12x+3x-9=\left(x-3\right)\left(4x+3\right)\\ l,=\left(x+5\right)^2-y^2=\left(x-y+5\right)\left(x+y+5\right)\\ m,=x^2-\left(2y-6\right)^2=\left(x-2y+6\right)\left(x+2y-6\right)\\ n,=\left(x^2+5x+4\right)\left(x^2+5x+6\right)-24\\ =\left(x^2+5x+5\right)^2-1-24\\ =\left(x^2+5x+5\right)^2-25\\ =\left(x^2+5x\right)\left(x^2+5x+10\right)\\ =x\left(x+5\right)\left(x^2+5x+10\right)\)
mn giải giúp em vơi ạ em đang cần gấp cảm ơn
26 tháng 5 2022
a,
Xét Δ ABH và Δ CBA, có :
\(\widehat{ABH}=\widehat{CAB}\) (góc chung)
\(\widehat{AHB}=\widehat{CAB}=90^o\)
=> Δ ABH ~ Δ CBA (g.g)
=> \(\dfrac{AB}{CB}=\dfrac{BH}{BA}\)
=> \(AB^2=BH.BC\)
Xét Δ ABC vuông tại A, có :
\(BC^2=AB^2+AC^2\) (Py - ta - go)
=> \(BC^2=15^2+20^2\)
=> BC = 25 (cm)
Ta có : \(AB^2=BH.BC\) (cmt)
=> \(15^2=BH.25\)
=> BH = 9 (cm)
Ta có : BC = BH + CH
=> 25 = 9 + CH
=> CH = 16 (cm)
26 tháng 5 2022
b,
Xét Δ AMN và Δ ACB, có :
\(\widehat{MAN}=\widehat{CAB}=90^o\)
\(\widehat{MAN}=\widehat{CAB}\) (góc chung)
=> Δ AMN ~ Δ ACB (g.g)
=> \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> AM.AB = AN.AC
Ta có : \(\dfrac{AM}{AC}=\dfrac{AN}{AB}\)
=> \(\dfrac{AB}{AC}=\dfrac{AN}{AM}\)
=> \(\dfrac{AN}{AM}=\dfrac{15}{20}=\dfrac{3}{4}\)
Vậy : ta có kết luận : Δ AMN = \(\dfrac{3}{4}\) Δ ACB
HM
2
14 tháng 3 2022
\(\dfrac{x-3}{3}=4-\dfrac{1-2x}{5}\)
=>5(x-3)=60-3(1-2x)
=>5x-15=60-3+6x
=>5x-15=6x+57
=>6x+57=5x-15
hay x=-72(nhận)
giúp em bài 1 dạng 3 vói em, em cần gấp lắm, em cảm ơn ạ
17 tháng 10 2021
Bài 1:
1) \(\Rightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
2) \(\Rightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
3) \(\Rightarrow\left(4x-3\right)\left(7-12x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{4}\\x=\dfrac{7}{12}\end{matrix}\right.\)
4) \(\Rightarrow x^3+8-x^3+25x=-17\)
\(\Rightarrow25x=-25\Rightarrow x=-1\)
5) \(\Rightarrow\left(3x-2\right)\left(3x+2\right)-2\left(3x-2\right)^2=0\)
\(\Rightarrow\left(3x-2\right)\left(3x+2-6x+4\right)=0\)
\(\Rightarrow\left(3x-2\right)\left(-3x+6\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=2\end{matrix}\right.\)
17 tháng 10 2021
Bài 3:
c: \(x^2+7x+12=\left(x+3\right)\left(x+4\right)\)
d: \(x^3-7x-6\)
\(=x\left(x-1\right)\left(x+1\right)-6\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2-x-6\right)\)
\(=\left(x+1\right)\left(x-3\right)\left(x+2\right)\)
23 tháng 7 2021
11)11) 3x(x-5)2-(x+2)3+2(x-1)3-(2x+1)(4x2-2x+1)=3x(x2-10x+25)-(x3+6x2+12x+8)+2(x3-3x2+3x-1)-(8x3+1)=3x3-30x2+75x-x3-6x2-12x-8+2x3-6x2+6x-2-8x3-1=-4x3-42x2+63x-11
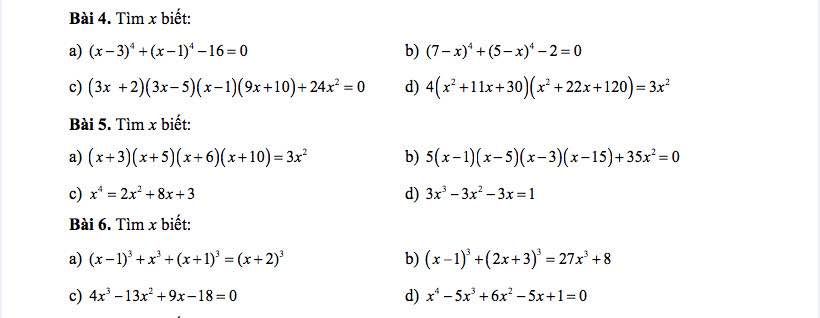
\(12x^2y^3-10x^2y^3:5x^2y^2+4xy\left(1-3xy\right)^2\)
\(=12x^2y^3-2y+4xy\left(1-6xy+9x^2y^2\right)\)
\(=12x^2y^3-2y+4xy-24x^2y^2+36x^3y^3\)