Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a)\(\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9x-18}+6\sqrt{\dfrac{x-2}{81}}=-4\) (đk: \(x\ge2\))
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-\dfrac{2}{3}\sqrt{9\left(x-2\right)}+\dfrac{6}{\sqrt{81}}\sqrt{x-2}=-4\)
\(\Leftrightarrow\dfrac{1}{3}\sqrt{x-2}-2\sqrt{x-2}+\dfrac{2}{3}\sqrt{x-2}=-4\)
\(\Leftrightarrow-\sqrt{x-2}=-4\) \(\Leftrightarrow x-2=16\)
\(\Leftrightarrow x=18\) (thỏa)
Vậy...
b)\(\sqrt{9x^2+12x+4}=4x\)(Đk:\(9x^2+12x+4\ge0\))
\(\Leftrightarrow\left\{{}\begin{matrix}4x\ge0\\9x^2+12x+4=16x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+12x+4=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\-7x^2+14x-2x+4=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left(x-2\right)\left(-7x-2\right)=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\\left[{}\begin{matrix}x=2\\x=-\dfrac{2}{7}\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow x=2\) (tm đk)
Vậy...
c) \(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}\) (đk: \(x\ge1\))
\(\Leftrightarrow x-2\sqrt{x-1}=x-1\)
\(\Leftrightarrow\sqrt{x-1}=\dfrac{1}{2}\) \(\Leftrightarrow x=\dfrac{5}{4}\) (tm)
Vậy...

\(A=4-\sqrt{21-8\sqrt{5}}=4-\sqrt{4^2-8\sqrt{5}+\left(\sqrt{5}\right)^2}.\)
\(A=4-\sqrt{\left(4-\sqrt{5}\right)^2}=4-\left(4-\sqrt{5}\right)\)
=> \(A=\sqrt{5}\)

1. \(=\sqrt{\left(\sqrt{\frac{7}{2}}+\sqrt{\frac{3}{2}}\right)^2}+\sqrt{\left(\sqrt{\frac{7}{2}}-\sqrt{\frac{3}{2}}\right)^2}-2\sqrt{4\sqrt{7}}=\frac{7}{2}+\frac{3}{2}+\frac{7}{2}-\frac{3}{2}-2\sqrt{4\sqrt{7}}\)
\(=7-2\sqrt{4\sqrt{7}}\)
cho hỏi tại sao có số \(\frac{7}{2};\frac{3}{2}\)zậy chỉ với

tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha

\(\frac{\sqrt{\sqrt{4+\sqrt{15}}+\sqrt{5-\sqrt{21}}}}{\sqrt{6+\sqrt{35}}}\)+\(\sqrt{\frac{1}{4-2\sqrt{3}}}\)-\(\sqrt{\frac{1}{4+2\sqrt{3}}}\)
=\(\frac{\sqrt{\sqrt{\frac{1}{2}\left(8+2\sqrt{15}\right)}+\sqrt{\frac{1}{2}\left(10-2\sqrt{21}\right)}}}{\sqrt{\frac{1}{2}\left(12+2\sqrt{35}\right)}}\)+\(\sqrt{\frac{1}{3-2\sqrt{3}.1+1}}\)-\(\sqrt{\frac{1}{3+2\sqrt{3}.1+1}}\)
=\(\frac{\sqrt{\sqrt{\frac{1}{2}\left(5+2\sqrt{5}.\sqrt{3}+3\right)}+\sqrt{\frac{1}{2}\left(7-2\sqrt{7}.\sqrt{3}+3\right)}}}{\sqrt{\frac{1}{2}\left(7+2\sqrt{7}.\sqrt{5}+5\right)}}\)+\(\sqrt{\frac{1}{\left(\sqrt{3}-1\right)^2}}\)-\(\sqrt{\frac{1}{\left(\sqrt{3}+1\right)^2}}\)
=\(\frac{\sqrt{\sqrt{\frac{1}{2}\left(\sqrt{5}+\sqrt{3}\right)^2}+\sqrt{\frac{1}{2}\left(\sqrt{7}-\sqrt{3}\right)^2}}}{\sqrt{\frac{1}{2}\left(\sqrt{7}+\sqrt{5}\right)^2}}\)+\(\frac{1}{\sqrt{3}-1}\)-\(\frac{1}{\sqrt{3}+1}\)
=\(\frac{\sqrt{\sqrt{\frac{1}{2}}.\left(\sqrt{5}+\sqrt{3}\right)+\sqrt{\frac{1}{2}}.\left(\sqrt{7}-\sqrt{3}\right)}}{\sqrt{\frac{1}{2}}.\left(\sqrt{7}+\sqrt{5}\right)}\)+\(\frac{\sqrt{3}+1-\sqrt{3}+1}{3-1}\)
=\(\frac{\sqrt{\sqrt{\frac{1}{2}}.\left(\sqrt{7}+\sqrt{5}\right)}}{\sqrt{\frac{1}{2}}.\left(\sqrt{7}+\sqrt{5}\right)}\)+1
=\(\frac{1}{\sqrt{\sqrt{\frac{1}{2}}.\left(\sqrt{7}+\sqrt{5}\right)}}\)+1

Ta có: \(\dfrac{8+2\sqrt{15}+\sqrt{21}+\sqrt{35}}{\sqrt{3}+\sqrt{5}+\sqrt{7}}\)
\(=\dfrac{\left(\sqrt{3}+\sqrt{5}\right)^2+\sqrt{7}\left(\sqrt{3}+\sqrt{5}\right)}{\sqrt{3}+\sqrt{5}+\sqrt{7}}\)
\(=1+\sqrt{3}+\sqrt{5}\)
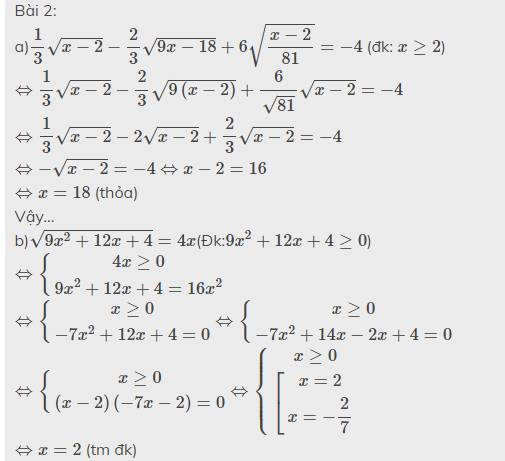
Bạn để ý nhé cách tính là nhân cả tử và mẫu với căn 2
1) \(=\frac{\sqrt{2}.\sqrt{5-\sqrt{21}}}{\sqrt{2}}\)
\(=\frac{\sqrt{10-2\sqrt{21}}}{\sqrt{2}}\)
\(=\frac{\sqrt{7-2\sqrt{21}+3}}{\sqrt{2}}\)
\(=\frac{\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}}{\sqrt{2}}\)
\(=\frac{\sqrt{7}-\sqrt{3}}{\sqrt{2}}\)
\(=\frac{\sqrt{14}-\sqrt{6}}{2}\)
câu 2 bạn làm tương tự nhé