Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.\) Ta có:
\(MTC:\) \(\left(x+1\right)\left(x+2\right)\)
Do đó
\(\frac{3x}{x+1}=\frac{3x\left(x+2\right)}{\left(x+1\right)\left(x+2\right)}\)
\(\frac{x+4}{x+2}=\frac{\left(x+1\right)\left(x+4\right)}{\left(x+1\right)\left(x+2\right)}\)
\(b.\) Ta có:
\(x^2+x=x\left(x+1\right)\)
\(x^2-1=\left(x-1\right)\left(x+1\right)\)
nên \(MTC:\) \(x\left(x-1\right)\left(x+1\right)\)
Do đó:
\(\frac{5}{x^2+x}=\frac{5}{x\left(x+1\right)}=\frac{5\left(x-1\right)}{x\left(x-1\right)\left(x+1\right)}\)
\(\frac{6}{x^2-1}=\frac{6}{\left(x-1\right)\left(x+1\right)}=\frac{6x}{x\left(x-1\right)\left(x+1\right)}\)
\(c.\) Ta có:
\(x^2-5x+4=x^2-x-4x+4=x\left(x-1\right)-4\left(x-1\right)=\left(x-1\right)\left(x-4\right)\)
\(2x^2-8x=2x\left(x-4\right)\)
nên \(MTC:\) \(2x\left(x-1\right)\left(x-4\right)\)
Do đó:
\(\frac{4}{x^2-5x+4}=\frac{4}{\left(x-1\right)\left(x-4\right)}=\frac{8x}{2x\left(x-1\right)\left(x-4\right)}\)
\(\frac{x+1}{2x^2-8x}=\frac{x+1}{2x\left(x-4\right)}=\frac{\left(x-1\right)\left(x+1\right)}{2x\left(x-1\right)\left(x-4\right)}\)
Làm nốt d :P
\(\frac{x+3}{2x^2-15x-8};\frac{3}{x^2-8x}\)
Ta có : \(2x^2-15x-8=\left(2x+1\right)\left(x-8\right)\)
\(x^2-8x=x\left(x-8\right)\)
MTC : \(x\left(x-8\right)\left(2x+1\right)\)
\(\frac{x+3}{2x^2-15x-8}=\frac{x+3}{\left(2x+1\right)\left(x-8\right)}=\frac{x^2+3x}{x\left(x-8\right)\left(2x+1\right)}\)
\(\frac{3}{x^2-8x}=\frac{3}{x\left(x-8\right)}=\frac{6x+3}{x\left(x-8\right)\left(2x+1\right)}\)

a,\(\frac{2x^2+4x}{x+2}\)=\(\frac{2x\left(x+2\right)}{x+2}\)\(=2x\)
b, \(\frac{3x}{2x+4}\)=\(\frac{3x^2-6x}{2\left(x+2\right)\left(x-2\right)}\)
\(\frac{x+3}{x^2+4}\)=\(\frac{2x+6}{2\left(x-2\right)\left(x+2\right)}\)
tick mình nhé!!

a kham khảo nha , e nhờ a e lm chứ ko phải e lm nha !
\(\left(x-2\right)\left(\frac{3}{x}+2-\frac{5}{2x}-4+\frac{8}{x^2}-4\right)\)
\(\left(x-2\right)\left[\left(\frac{3}{x}-\frac{5}{2x}\right)-6+\frac{8}{x^2}\right]\)
\(\left(x-2\right)\left(\frac{1}{2x}-6+\frac{8}{x^2}\right)\)
\(\left(x-2\right)\left(\frac{3}{x+2}-\frac{5}{2x-4}+\frac{8}{x^2-4}\right)\)
\(=\left(x-2\right)\left[\frac{3}{x+2}-\frac{5}{2\left(x-2\right)}+\frac{8}{\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{3.2\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{8.2}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)}{2\left(x-2\right)\left(x+2\right)}-\frac{5\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}+\frac{16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\left(x-2\right)\left[\frac{6\left(x-2\right)-5\left(x+2\right)+16}{2\left(x-2\right)\left(x+2\right)}\right]\)
\(=\frac{\left(x-2\right)\left(x-6\right)}{2\left(x-2\right)\left(x+2\right)}\)
\(=\frac{x-6}{2\left(x+2\right)}\)

a) Tìm MTC: x3 – 1 = (x – 1)(x2 + x + 1)
Nên MTC = (x – 1)(x2 + x + 1)
Nhân tử phụ:
(x3 – 1) : (x3 – 1) = 1
(x – 1)(x2 + x + 1) : (x2 + x + 1) = x – 1
(x – 1)(x2+ x + 1) : 1 = (x – 1)(x2 + x + 1)
Qui đồng:
b) Tìm MTC: x + 2
2x – 4 = 2(x – 2)
6 – 3x = 3(2 – x)
MTC = 6(x – 2)(x + 2)
Nhân tử phụ:
6(x – 2)(x + 2) : (x + 2) = 6(x – 2)
6(x – 2)(x + 2) : 2(x – 2) = 3(x + 2)
6(x – 2)(x + 2) : -3(x – 2) = -2(x + 2)
Qui đồng:



6:
a: ĐKXĐ: x<>0
\(\dfrac{x^3+3x^2+3x+1}{x^2+x}\)
\(=\dfrac{\left(x+1\right)^3}{x\left(x+1\right)}=\dfrac{\left(x+1\right)^2}{x}\)
b: ĐKXĐ: x<>1
\(\dfrac{x^3-3x^2+3x-1}{2x-2}\)
\(=\dfrac{\left(x-1\right)^3}{2\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{2}\)
c: ĐKXĐ: x<>-2
\(\dfrac{x^2+4x+4}{2x+4}\)
\(=\dfrac{\left(x+2\right)^2}{2\left(x+2\right)}\)
\(=\dfrac{x+2}{2}\)
d: ĐKXĐ: x<>-2
\(\dfrac{\left(x-1\right)\left(-x-2\right)}{x+2}\)
\(=\dfrac{\left(-x+1\right)\left(x+2\right)}{x+2}=-x+1\)
e: ĐKXĐ: x<>-y
\(\dfrac{x^2-y^2}{x+y}=\dfrac{\left(x-y\right)\left(x+y\right)}{x+y}=x-y\)
g: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{-3x^2-6x}{4-x^2}=\dfrac{3x^2+6x}{x^2-4}\)
\(=\dfrac{3x\left(x+2\right)}{\left(x+2\right)\cdot\left(x-2\right)}=\dfrac{3x}{x-2}\)
7:
a: \(\dfrac{2}{5x^3y^2}=\dfrac{2\cdot4}{20x^3y^2}=\dfrac{8}{20x^3y^2}\)
\(\dfrac{3}{4xy}=\dfrac{3\cdot5\cdot x^2y}{20x^3y^2}=\dfrac{15x^2y}{20x^3y^2}\)
b: \(\dfrac{x}{x^2-2xy+y^2}=\dfrac{x}{\left(x-y\right)^2}\)
\(\dfrac{x}{x^2-xy}=\dfrac{x}{x\left(x-y\right)}=\dfrac{1}{x-y}=\dfrac{\left(x-y\right)}{\left(x-y\right)^2}\)
c: \(\dfrac{1}{x+2}=\dfrac{6}{6\left(x+2\right)}\)
\(\dfrac{2}{2x+4}=\dfrac{2}{2\left(x+2\right)}=\dfrac{1}{x+2}=\dfrac{6}{6\left(x+2\right)}\)
\(\dfrac{3}{3x+6}=\dfrac{3}{3\left(x+2\right)}=\dfrac{6}{6\left(x+2\right)}\)
d:
\(\dfrac{2}{2x-6}=\dfrac{2}{2\left(x-3\right)}=\dfrac{1}{x-3};\dfrac{3}{3x-9}=\dfrac{3}{3\left(x-3\right)}=\dfrac{1}{x-3}\)
\(\dfrac{2}{2x-6}=\dfrac{1}{x-3}=\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}\)
\(\dfrac{3}{3x-9}=\dfrac{1}{x-3}=\dfrac{x+3}{\left(x-3\right)\left(x+3\right)}\)
\(\dfrac{1}{x+3}=\dfrac{x-3}{\left(x+3\right)\left(x-3\right)}\)

cho mình hỏi là giữa khác phân số với nhua là phải có dấu như là công, trừ, nhân hay chia chứ?

\(\)\(a)\frac{1}{{4{\rm{x}}{y^2}}}\)và \(\frac{5}{{6{{\rm{x}}^2}y}}\)
Ta có: MTC là : \(12{{\rm{x}}^2}{y^2}\).
Nhân tử phụ của phân thức \(\frac{1}{{4{\rm{x}}{y^2}}}\)là 3x
Nhân tử phụ của phân thức \(\frac{5}{{6{{\rm{x}}^2}y}}\)là 2y
Khi đó: \(\frac{1}{{4{\rm{x}}{y^2}}} = \frac{{1.3{\rm{x}}}}{{4{\rm{x}}{y^2}.3{\rm{x}}}} = \frac{{3{\rm{x}}}}{{12{{\rm{x}}^2}{y^2}}}\)
\(\frac{5}{{6{{\rm{x}}^2}y}} = \frac{{5.2y}}{{6{{\rm{x}}^2}y.2y}} = \frac{{10y}}{{12{{\rm{x}}^2}{y^2}}}\)
\(b)\frac{9}{{4{{\rm{x}}^2} - 36}}\)và \(\frac{1}{{{x^2} + 6{\rm{x}} + 9}}\).
Ta có: \(\begin{array}{l}4{{\rm{x}}^2} - 36 = 4({x^2} - 9) = 4(x - 3)(x + 3)\\{x^2} + 6{\rm{x}} + 9 = {(x + 3)^2}\end{array}\)
MTC là: \(4(x - 3){(x + 3)^2}\)
Nhân tử phụ của phân thức \(\frac{9}{{4{{\rm{x}}^2} - 36}}\)là: x + 3
Nhân tử phụ của phân thức \(\frac{1}{{{x^2} + 6{\rm{x}} + 9}}\)là 4(x – 3)
Khi đó: \(\begin{array}{l}\frac{9}{{4{{\rm{x}}^2} - 36}} = \frac{9}{{4({x^2} - 9)}} = \frac{9}{{4(x - 3)(x + 3)}} = \frac{{9(x + 3)}}{{4(x - 3){{(x + 3)}^2}}}\\\frac{1}{{{x^2} + 6{\rm{x}} + 9}} = \frac{1}{{{{(x + 3)}^2}}} = \frac{{4(x - 3)}}{{4(x - 3){{(x + 3)}^2}}}\end{array}\)
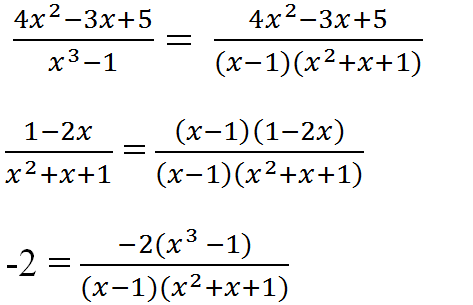
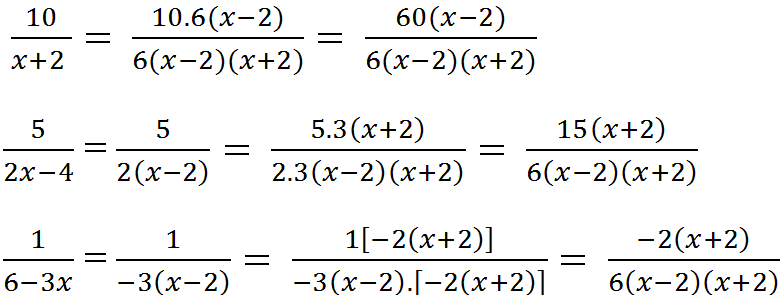
Rút gọn