
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

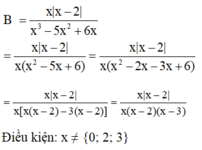
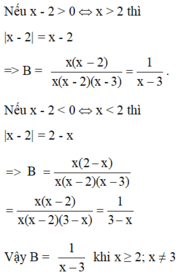
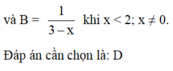

Giải như sau.
(1)+(2)⇔x2−2x+1+√x2−2x+5=y2+√y2+4⇔(x2−2x+5)+√x2−2x+5=y2+4+√y2+4⇔√y2+4=√x2−2x+5⇒x=3y(1)+(2)⇔x2−2x+1+x2−2x+5=y2+y2+4⇔(x2−2x+5)+x2−2x+5=y2+4+y2+4⇔y2+4=x2−2x+5⇒x=3y
⇔√y2+4=√x2−2x+5⇔y2+4=x2−2x+5, chỗ này do hàm số f(x)=t2+tf(x)=t2+t đồng biến ∀t≥0∀t≥0
Công việc còn lại là của bạn !
\(\left(x+6\right)\left(2x+1\right)=0\)
<=> \(\orbr{\begin{cases}x+6=0\\2x+1=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=-6\\x=-\frac{1}{2}\end{cases}}\)
Vậy....
hk tốt
^^

Bài 1.
a) ( x3 - 8) : ( x2 + 2x + 4 )
= ( x - 2)( x2 + 2x + 4 ) : ( x2 + 2x + 4 )
= x - 2
b) ( 3x2 - 6x ) : ( 2 - x)
= 3x( x - 2) : ( 2 - x)
= -3x( 2 - x ) : ( 2 - x)
= - 3x
Bài 2 .
\(\dfrac{2x-1}{x^2-x}\)
a) Để A có nghĩa tức là A xác định :
ĐKXĐ : x( x - 1) # 0
=> x # 0 ; x # 1
Vậy,...
b) Vì : x = 0 không thỏa mãn ĐKXĐ nên tại x = 0 giá trị của A không xác định
Vì : x = 3 thỏa mãn ĐKXĐ nên ta thay x = 3 vào A , ta có :
\(A=\dfrac{2.3-1}{3^2-3}=\dfrac{5}{6}\)
Vậy , tại : x = 3 thì A = \(\dfrac{5}{6}\)
Bài 3 .
a) ( 6x + 1)2 + ( 6x - 1)2 - 2( 1 + 6x )( 6x - 1)
= ( 6x + 1)2 - 2( 1 + 6x )( 6x - 1) + ( 6x - 1)2
= ( 6x + 1 - 6x + 1)2
= 1
b) 3( 22 + 1)( 24 + 1)( 28 + 1)( 216 + 1)
= ( 22 - 1)( 22 + 1)( 24 + 1)( 28 + 1)( 216 + 1)
= ( 24 - 1)( 24 + 1)( 28 + 1)( 216 + 1)
= ( 28 - 1)( 28 + 1)( 216 + 1)
= ( 216 - 1)( 216 + 1)
= 232 - 1
c) x( 2x2 - 3) - x2( 5x + 3 ) + 3x2
= 2x3 - 3x - 5x3 - 3x2 + 3x2
= - 3x3 - 3x
d) 3x( x - 2) - 5x( 1 - x) - 8( x2 - 3)
= 3x2 - 6x - 5x + 5x2 - 8x2 + 24
= -11x + 24

b: \(=\dfrac{4x\left(x-1\right)\left(x+1\right)}{6x\left(x-1\right)}=\dfrac{2\left(x+1\right)}{3}\)
c: \(=\dfrac{\left(5-x-1\right)\left(5+x+1\right)}{\left(x+6\right)^2}=\dfrac{\left(4-x\right)\left(x+6\right)}{\left(x+6\right)^2}=\dfrac{4-x}{x+6}\)
d: \(=\dfrac{\left(x+2\right)\left(x+3\right)}{\left(x+2\right)^2}=\dfrac{x+3}{x+2}\)

a) (6x+1)2 + (6x-1)2 - 2(1+6x)(6x-1)
= (6x+1+6x-1)2
=144x2
b) x(2x2 -3) - x2(5x+1) +x2
=2x3 - 3x - 5x3 -x2+x2
=-3x3-3x
=-3x(x2+1)
c) 3(22+1)(24+1)(28+1)(216+1)
= (22-1)(22+1)(24+1)(28+1)(216+1)
= (24-1)(24+1)(28+1)(216+1)
= (28-1)(28+1)(216+1)
= (216-1)(216+1)
= 232 -1
d) 3x(x-2) - 5x(1-x) - 8(x2 -3)
= 3x2-6x - 5x + 5x2 - 8x2 +24
= -11x +24

c. x^2-5x +6 = 0
<=> x^2 - 5x = -6
<=> - 4x = -6
<=> x= -6/-4
Mình chỉ phân tích đa thức thành nhân tử thôi , phần còn lại bạn tự tính nha keo dài lắm
A) 2x2(x+3) - x(x+3) = 0 <=> x(x - 3)(2x-1)=0
B) (2x+5)2 - (x+2)2=0 <=> (x+3)(3x+7)=0
C) (x2-2x) - (3x-6)=0 <=> (x-2)(x-3)=0
D) (2x-7)(2x-7-6x+18)=0 <=> (2x-7)(-4x+11)=0
E) (x-2)(x+1) - (x-2)(x+2)=0 <=> (x-2)*(-1)=0 <=> x-2=0
G) (2x-3)(2x+2-5x)=0 <=> (2x-3)(-3x+2)=0
H) (1-x)(5x+3+3x-7)=0 <=> (1-x)(8x-4)=0
F) (x+6)*3x=0
I) (x-3)(4x-1-5x-2)=0 <=> (x-3)(-x-3)=0
K) (x+4)(5x+8)=0
H) (x+3)(4x-9)=0

c. x^2-5x+6=0
<=> x^2-5x=-6
<=> -4x=-6
<=> x=-6/-4
vậy tập nghiệm của pt là s={-6/-4}

ChươngII *Dạng toán rútg gọn phân thức
Bài 1.Rút gọn phân thức
a. \(\dfrac{3x\left(1-x\right)}{2\left(x-1\right)}=\dfrac{-3x\left(x-1\right)}{2\left(x-1\right)}=-\dfrac{3x}{2}\)
b.\(\dfrac{6x^2y^2}{8xy^5}=\dfrac{3x.2xy^2}{4y^3.2xy^2}=\dfrac{3x}{4y^3}\)
c.\(\dfrac{23\left(x-y\right)\left(x-z\right)^2}{6\left(x-y\right)\left(x-z\right)}=\dfrac{23\left(x-z\right)}{6}\)
Bài 2 rút gọn các phân thức sau:
a.\(\dfrac{x^2-16}{4x-x^2}=\dfrac{\left(x-4\right)\left(x+4\right)}{-x\left(x-4\right)}=-\dfrac{x+4}{x}\)(x khác 0,x khác 4)
b.\(\dfrac{x^2+4x+3}{2x+6}=\dfrac{x^2+3x+x+3}{2\left(x+3\right)}=\dfrac{\left(x+3\right)\left(x+1\right)}{2\left(x+3\right)}=\dfrac{x+1}{2}\)
( x \(\ne-3\) )
c.\(\dfrac{15x\left(x+y\right)^3}{5y\left(x+y\right)^2}=\dfrac{3x\left(x+y\right)}{y}\) (y+(x+y) khác 0)
d. \(\dfrac{5\left(x-y\right)-3\left(y-x\right)}{10\left(x-y\right)}=\dfrac{5\left(x-y\right)+3\left(x-y\right)}{10\left(x-y\right)}=\dfrac{8\left(x-y\right)}{10\left(x-y\right)}=\dfrac{4}{5}\)
(x khác y)
e.\(\dfrac{2x+2y+5x+5y}{2x+2y-5x-5y}=\dfrac{2\left(x+y\right)+5\left(x+y\right)}{2\left(x+y\right)-5\left(x+y\right)}=\dfrac{7\left(x+y\right)}{-3\left(x+y\right)}=-\dfrac{7}{3}\)
(x khác -y)
f.\(\dfrac{x^2-xy}{3xy-3y^2}=\dfrac{x\left(x-y\right)}{3y\left(x-y\right)}=\dfrac{x}{3y}\)(x khác y,y khác 0)
g.\(\dfrac{2ax^2-4ax+2a}{5b-5bx^2}=\dfrac{2a\left(x^2-2x+1\right)}{-5b\left(x^2-1\right)}=\dfrac{2a\left(x-1\right)^2}{-5b\left(x-1\right)\left(x+1\right)}=\dfrac{2a\left(x-1\right)}{-5b\left(x+1\right)}\)
\ (b khác 0,x khác +-1)
h. \(\dfrac{4x^2-4xy}{5x^3-5x^2y}=\dfrac{4x\left(x-y\right)}{5x^2\left(x-y\right)}=\dfrac{4x}{5x^2}\)
(x khác 0,x khác y)
i.\(\dfrac{\left(x+y\right)^2-z^2}{x+y+z}=\dfrac{\left(x+y+z\right)\left(x+y-z\right)}{x+y+z}=x+y-z\)
(x+y+z khác 0)
k.\(\dfrac{x^6+2x^3y^3+y^6}{x^7-xy^6}=\dfrac{\left(x^3\right)^2+2x^3y^3+\left(y^3\right)^2}{x\left(x^6-y^6\right)}=\dfrac{\left(x^3+y^3\right)^2}{x\left(x^3-y^3\right)\left(x^3+y^3\right)}=\dfrac{x^3+y^3}{x\left(x^3-y^3\right)}\)
(x khác 0,x khác +-y)

1.a)\(20x-5y=5\left(4x-y\right)\)
b)\(5x\left(x-1\right)-3x\left(x-1\right)=\left(5x-3x\right)\left(x-1\right)=2x\left(x-1\right)\)
c)\(x\left(x+y\right)-6x-6y=x\left(x+y\right)-6\left(x+y\right)=\left(x-6\right)\left(x+y\right)\)
d)\(6x^3-9x^2=3x^2\left(2x-3\right)\)
e)\(4x^2y-8xy^2+10x^2y^2=2xy\left(2x-8y+10xy\right)\)
g)\(20x^2y-12x^3=4x^2\left(5y-3x\right)\)
h)\(8x^4+12x^2y-16x^3y^4=4x^2\left(2x^2+12y-16xy^4\right)\)
2.a)\(3x\left(x+1\right)-5y\left(x+1\right)=\left(3x-5y\right)\left(x+1\right)\)
b)\(3x\left(x-6\right)-2\left(x-6\right)=\left(3x-2\right)\left(x-6\right)\)
c)\(4y\left(x-1\right)-\left(1-x\right)=4y\left(x-1\right)+\left(x-1\right)=\left(4y+1\right)\left(x-1\right)\)
d)\(\left(x-3\right)^3+3-x=\left(x-3\right)^3-\left(x-3\right)=\left(x-3\right)\left[\left(x-3\right)^2-1\right]=\left(x-3\right)\left(x-2\right)\left(x-4\right)\)
e)\(7x\left(x-y\right)-\left(y-x\right)=7x\left(x-y\right)+\left(x-y\right)=\left(7x+1\right)\left(x-y\right)\)
h)\(3x^3\left(2y-3z\right)-15x\left(2y-3z\right)^2=3x\left(2y-3z\right)\left[x^2-5\left(2y-3z\right)\right]\)
k)Sai đề: \(3x\left(z+2\right)+5\left(-z-2\right)=3x\left(z+2\right)-5\left(z+2\right)=\left(3x-5\right)\left(z+2\right)\)
l)\(18x^2\left(3+x\right)+3\left(x+3\right)=3\left(x+3\right)\left(6x^2+1\right)\)
m)\(14x^2y-21xy^2+28x^2y^2=7xy\left(2x-3y+4xy\right)\)
n)\(10x\left(x-y\right)-8y\left(y-x\right)=10x\left(x-y\right)+8y\left(x-y\right)=2\left(5x+4y\right)\left(x-y\right)\)