LN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
J
6 tháng 9 2016
a)\(\frac{195}{260}=\frac{3}{4}\)
b)\(\frac{224224}{192192}=\frac{224}{192}=\frac{7}{6}\)
c)\(\frac{18}{32}=\frac{9}{16}\)
d)\(\frac{20062006}{20042004}=\frac{2006}{2004}=\frac{1003}{1002}\)
6 tháng 9 2016
cứ chia từ từ cho đến khi không chia được nữa thì toi gian k chỗ mình nhìu nha!!!
CM
19 tháng 3 2019
a) Các phân số tối giản vì tử số và mẫu số của chúng không cùng chia hết cho số hơn lơn 1 ( hoặc vì ta không thể rút gọn được các phân số đó nữa):
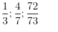
b) Phân số rút gọn :
DV
Đặng Việt Dũng
VIP
14 tháng 2 2023
Các phân số tối giản là: \(\dfrac{2}{3}\); \(\dfrac{4}{9}\)
Các phân số rút gọn được là: \(\dfrac{3}{18}=\dfrac{3:3}{18:3}=\dfrac{1}{6}\); \(\dfrac{9}{21}=\dfrac{9:9}{21:9}=\dfrac{1}{3}\); \(\dfrac{21}{45}=\dfrac{21:3}{45:3}=\dfrac{7}{15}\)
VN
Võ Ngọc Phương
VIP
14 tháng 2 2023
+ 2/5, 4/9 là những phân số tối giản
vì các phân số này ko thể rút gọn được nữa.
+ 3/18= 3:3/18:3= 1/6
9/21= 9:3/21:3= 3/7
21/45= 21:3/45:3= 7/15
chúc bạn học tốt!!!
2 tháng 3 2022
\(a,\\ =\dfrac{5}{4}-\dfrac{3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\\ b,\\ =\dfrac{2}{3}-\dfrac{2}{5}=\dfrac{10-6}{15}=\dfrac{4}{15}\\ c,\\ =\dfrac{5}{6}-\dfrac{1}{4}=\dfrac{20-6}{24}=\dfrac{14}{24}=\dfrac{7}{12}\\ d,\\ =\dfrac{4}{3}-\dfrac{1}{4}=\dfrac{12-3}{12}=\dfrac{9}{12}=\dfrac{3}{4}\)
15 tháng 7 2018
Tử số chưa rút gọn là :
165 : ( 7 + 4 ) x 7 = 105
Mẫu số chưa rút gọn là :
165 - 105 = 60
Phân số chưa rút gọn là \(\frac{105}{60}\)
NL
4
S
5 tháng 2 2023
\(\dfrac{50}{60}=\dfrac{5}{6}\)
\(\dfrac{33}{11}=3\)
\(\dfrac{16}{60}=\dfrac{4}{15}\)
\(\dfrac{42}{22}=\dfrac{21}{11}\)
22 tháng 3 2016
Gọi phân số đó là : a / b
ta có : a/b = 7/13
13*a=7*b
b =13*a : 7
vì tổng tử số và mẫu số là 4190
nên : a+ b= 4190
a+ 13* a : 7 =4190
7* a+ 13* a =29330
20 * a = 29330
a = 1466,5
b= 4190 - a = 4190 -1466,5 = 2723,5
22 tháng 3 2016
Tử số của phân số ứng với 7 phần còn mẫu ứng với 13 phần
4190 ứng với:
7+13=20(phần)
1 phần ứng với:
4190:20=209,5
Tử số là:
209,5x7=1466,5
Mẫu số là:
209,5x13=2723,5
Vậy phân số chưa rút gọn là: 1466,4/2723,5
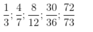
mình đang cần vội
a, Cho mk sửa đề
\(\frac{145145}{607607}=\frac{145.1001}{107.1001}=\frac{145}{607}\)
b, \(\frac{19491949}{20062006}=\frac{1949.10001}{2006.10001}=\frac{1949}{2006}\)