GP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PM
5
NN
2
MN
31 tháng 3 2021
\(a.-\dfrac{8}{12}=\dfrac{-2\cdot4}{4\cdot3}=-\dfrac{2}{3}\)
\(b.\dfrac{15}{-60}=\dfrac{15}{15\cdot-4}-\dfrac{1}{4}\)
\(c.\dfrac{-16}{-72}=\dfrac{-2\cdot8}{-9\cdot8}=\dfrac{2}{9}\)
\(d.\dfrac{35}{14\cdot15}=\dfrac{7\cdot5}{7\cdot2\cdot5\cdot3}=\dfrac{1}{6}\)
AL
31 tháng 3 2021
\(\dfrac{8}{12}\)=\(\dfrac{2}{31}\)
\(\dfrac{15}{-60}\)=\(\dfrac{-1}{4}\)
\(\dfrac{-16}{72}\)=\(\dfrac{-2}{9}\)
\(\dfrac{35}{14.15}=\dfrac{35}{210}=\dfrac{1}{6}\)
CM
4 tháng 3 2018
a ) − 18 − 27 = ( − 18 ) : ( − 9 ) ( − 27 ) : ( − 9 ) = 2 3
b ) 45 − 24 = 45 : ( − 3 ) ( − 24 ) : ( − 3 ) = − 15 8
PT
1
CM
5 tháng 1 2020
a) 36 − 48 = − 3 4
b) − 15 50 = − 3 10
c) − 18 − 81 = 2 9
d) 145 215 = 29 43
15 tháng 3 2021
b) \(\dfrac{6\cdot9-2\cdot17}{63\cdot3-119}\)
\(=\dfrac{2\left(3\cdot9-17\right)}{7\cdot\left(3\cdot9-17\right)}\)
\(=\dfrac{2}{7}\)
HQ
Hà Quang Minh
Giáo viên
2 tháng 10 2023
a) \(\dfrac{{50}}{{85}}\)
Ta có: \(50 =2.5^2; 85= 5.17\)
Thừa số nguyên tố chung là 5 với số mũ nhỏ nhất là 1 nên ƯCLN(50, 85) = 5. Do đó, \(\dfrac{{50}}{{85}}\) chưa là phân số tối giản
Ta có: \(\dfrac{{50}}{{85}} = \dfrac{{50:5}}{{85:5}} = \dfrac{{10}}{{17}}\)
b)\(\dfrac{{23}}{{81}}\)
Ta có: \(23 = 23; 81 = 3^4\)
Chúng không có thừa số nguyên tố chung nên ƯCLN(23, 81) = 1. Do đó, \(\dfrac{{23}}{{81}}\) là phân số tối giản.
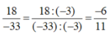
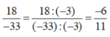
\(\frac{2^{10}\cdot3^{10}-2^{10}\cdot3^9}{2^9\cdot3^{10}}=\frac{2^{10}\cdot\left[3^9\left(3-1\right)\right]}{2^9\cdot3^{10}}\)
\(=\frac{2^{10}\cdot3^9\cdot2}{2^9\cdot3^{10}}=\frac{2^2}{3}=\frac{4}{3}\)
\(\frac{68\cdot15-18}{50+68\cdot14}=\frac{68\cdot\left(14+1\right)-18}{50+68\cdot14}\)
\(=\frac{68\cdot14+68-18}{50+68\cdot14}=\frac{68\cdot14+50}{50+68\cdot14}=1\)
Thank you. Mình cx đang nghĩ z