
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

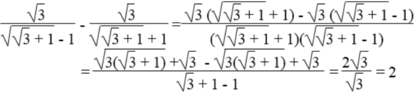

\(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}-\frac{3-\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{3+\sqrt{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)
a, \(\frac{1}{3-\sqrt{7}}-\frac{1}{3+\sqrt{7}}=\frac{3+\sqrt[]{7}-3+\sqrt{7}}{\left(3-\sqrt{7}\right)\left(3+\sqrt{7}\right)}\)
\(=\frac{2\sqrt{7}}{9-7}=\sqrt{7}\)

\(\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}-\dfrac{\sqrt{3}}{\sqrt{\sqrt{3}-1}+1}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}+1\right)}{\sqrt{3}}-\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}-1}-1\right)}{\sqrt{3}}=\dfrac{\sqrt{3}\left(\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\right)}{\sqrt{3}}=\sqrt{\sqrt{3}+1}-\sqrt{\sqrt{3}-1}+2\)

a: \(=\sqrt{3}-1-\sqrt{3}=-1\)
b: \(=2\sqrt{3}-10\sqrt{3}+4\sqrt{3}=-4\sqrt{3}\)

\(\dfrac{3}{\sqrt{3}+1}-\dfrac{3}{\sqrt{3}-1}\)
\(=\dfrac{3\left(\sqrt{3}-1\right)-3\left(\sqrt{3}+1\right)}{3-1}\)
\(=\dfrac{3\sqrt{3}-3-3\sqrt{3}-3}{2}=\dfrac{-6}{2}=-3\)

a)
\(2\sqrt{5}\)+ I1-\(\sqrt{5}\)I
\(2\sqrt{5}\)+1-\(\sqrt{5}\)
1+\(\sqrt{5}\)
b: \(=\dfrac{\sqrt{3}-1+\sqrt{3}+1-4\sqrt{3}}{2}=-\sqrt{3}\)

Lời giải:
a.
\(B=\frac{3+\sqrt{x}-(3-\sqrt{x})}{(3-\sqrt{x})(3+\sqrt{x})}.\frac{3+\sqrt{x}}{\sqrt{x}}=\frac{2\sqrt{x}}{(3-\sqrt{x})(3+\sqrt{x})}.\frac{3+\sqrt{x}}{\sqrt{x}}\\ =\frac{2}{3-\sqrt{x}}\)
b.
Để $B=\frac{2}{3-\sqrt{x}}>0\Leftrightarrow 3-\sqrt{x}>0$
$\Leftrightarrow \sqrt{x}<3$
$\Leftrightarrow 0< x< 9$
Kết hợp với đkxđ suy ra mọi số thực $x$ thỏa mãn $0< x< 9$ thỏa mãn đề.

\(\dfrac{1}{\sqrt{3}+1}+\dfrac{1}{\sqrt{3}-1}-2\sqrt{3}\)
\(=\dfrac{\sqrt{3}-1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}+\dfrac{\sqrt{3}+1}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}-2\sqrt{3}\)
\(=\dfrac{\sqrt{3}-1+\sqrt{3}+1}{3-1}-2\sqrt{3}\)
\(=\dfrac{2\sqrt{3}}{2}-2\sqrt{3}\)
\(=\sqrt{3}-2\sqrt{3}=-\sqrt{3}\)