Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Ta có: \(\left\{{}\begin{matrix}2x+y=5\\3x-2y=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}6x+3y=15\\6x-4y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}7y=-7\\2x+y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-1\\2x=5-y=5-\left(-1\right)=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-1\end{matrix}\right.\)
2) Ta có: \(B=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{5\sqrt{x}+2}{4-x}\right):\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x+3\sqrt{x}+2+2\sqrt{x}\left(\sqrt{x}-2\right)-5\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}:\dfrac{1}{\sqrt{x}+2}\)
\(=\dfrac{x-2\sqrt{x}+2x-4\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}+2}{1}\)
\(=\dfrac{3x-6\sqrt{x}}{\sqrt{x}-2}\)
\(=3\sqrt{x}\)

`B=(1/(3-sqrtx)-1/(3+sqrtx))*(3+sqrtx)/sqrtx(x>=0,x ne 9)`
`B=((3+sqrtx)/(9-x)-(3-sqrtx)/(9-x))*(3+sqrtx)/sqrtx`
`B=((3+sqrtx-3+sqrtx)/(9-x))*(3+sqrtx)/sqrtx`
`B=(2sqrtx)/((3-sqrtx)(3+sqrtx))*(3+sqrtx)/sqrtx`
`B=2/(3-sqrtx)`
`B>1/2`
`<=>2/(3-sqrtx)-1/2>0`
`<=>(4-3+sqrtx)/[2(3-sqrtx)]>0`
`<=>(sqrtx+1)/(2(3-sqrtx))>0`
Mà `sqrtx+1>=1>0`
`<=>2(3-sqrtx)>0`
`<=>3-sqrtx>0`
`<=>sqrtx<3`
`<=>x<9`

Đk:\(x>0;x\ne1\)
\(B=\left[\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right]:\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(x-1\right)}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}.\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{1}{\sqrt{x}-1}\)
\(B=\dfrac{1}{2}\Leftrightarrow\dfrac{1}{\sqrt{x}-1}=\dfrac{1}{2}\Leftrightarrow\sqrt{x}-1=2\)\(\Leftrightarrow x=9\) (tm)
Vậy..
a) \(B=\left(\dfrac{1}{x-\sqrt{x}}+\dfrac{\sqrt{x}}{x-1}\right):\dfrac{x\sqrt{x}-1}{x\sqrt{x}-\sqrt{x}}\)
\(B=\dfrac{\sqrt{x}+1+x}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(B=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(B=\dfrac{1}{\sqrt{x}-1}\)
b) Với \(B=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{x}-1}=\dfrac{1}{2}\Leftrightarrow\sqrt{x}-1=2\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\)
Vậy...
Chúc bạn học tốt

\(=>B=\dfrac{\left(\sqrt{x}-1\right)\sqrt{x}-5\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(B=\dfrac{x-\sqrt{x}-5\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{x-6\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(B=\dfrac{\left(\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-4}{\sqrt{x}}\)
Ta có: \(B=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}-\dfrac{5\sqrt{x}-8}{x-2\sqrt{x}}\)
\(=\dfrac{x-\sqrt{x}-5\sqrt{x}+8}{\sqrt{x}\cdot\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-6\sqrt{x}+8}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-4}{\sqrt{x}-2}\)

\(B=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{x+1}{x-1}=\dfrac{\sqrt{x}+1-\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{x-1}{x+1}\)
\(=\dfrac{2}{x-1}.\dfrac{x-1}{x+1}=\dfrac{2}{x+1}\)
Để \(B< 1\Rightarrow\dfrac{2}{x+1}< 1\Rightarrow1-\dfrac{2}{x+1}>0\Rightarrow\dfrac{x-1}{x+1}>0\)
mà \(x+1>0\left(x\ge0\right)\Rightarrow x-1>0\Rightarrow x>1\)

a) Ta có: \(A=3\sqrt{2x}-5\sqrt{8x}+7\sqrt{18x}+30\)
\(=3\sqrt{2x}-10\sqrt{2x}+21\sqrt{2x}+30\)
\(=14\sqrt{2x}+30\)
b) Ta có: \(B=4\sqrt{\dfrac{25x}{4}}-\dfrac{8}{3}\sqrt{\dfrac{9x}{4}}-\dfrac{4}{3x}\cdot\sqrt{\dfrac{9x^3}{64}}\)
\(=4\cdot\dfrac{5\sqrt{x}}{2}-\dfrac{8}{3}\cdot\dfrac{3\sqrt{x}}{2}-\dfrac{4}{3x}\cdot\dfrac{3x\sqrt{x}}{8}\)
\(=10\sqrt{x}-4\sqrt{x}-\dfrac{1}{2}\sqrt{x}\)
\(=\dfrac{11}{2}\sqrt{x}\)
c) Ta có: \(\dfrac{y}{2}+\dfrac{3}{4}\sqrt{9y^2-6y+1}-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}\left(1-3y\right)-\dfrac{3}{2}\)
\(=\dfrac{1}{2}y+\dfrac{3}{4}-\dfrac{9}{4}y-\dfrac{3}{2}\)
\(=-\dfrac{7}{4}y-\dfrac{3}{4}\)

Sửa đề: \(A=\dfrac{1-3x}{2y}\cdot\sqrt{\dfrac{36y^2}{9x^2-6x+1}}\)
\(=\dfrac{1-3x}{2y}\cdot\sqrt{\left(\dfrac{6y}{3x-1}\right)^2}\)
\(=\dfrac{1-3x}{2y}\cdot\left|\dfrac{6y}{3x-1}\right|\)
x>1/3 nên 3x-1>0
y>0 nên 6y>0
=>\(A=\dfrac{1-3x}{2y}\cdot\dfrac{6y}{3x-1}=-3y\)

ĐKXĐ: \(x\ge0;x\ne9\)
\(B=\left(\dfrac{1}{\sqrt{x}+3}+\dfrac{3}{x-9}\right):\dfrac{1}{\sqrt{x}-3}\)
\(=\left[\dfrac{\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}+\dfrac{3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\right]:\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}.\dfrac{\sqrt{x}-3}{1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >9\end{matrix}\right.\)
\(B=\dfrac{\sqrt{x}-3+3}{x-9}\cdot\left(\sqrt{x}-3\right)=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)

Câu 1:
Sửa đề: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
Ta có: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{1}{\sqrt{x}+3}\right):\left(\dfrac{x+3\sqrt{x}-2\left(\sqrt{x}+3\right)+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}:\dfrac{x+3\sqrt{x}-2\sqrt{x}-6+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x+\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=1\)
Câu 3:
Ta có: \(Q=\left(\dfrac{a}{a-2\sqrt{a}}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{a-4\sqrt{a}+4}\)
\(=\left(\dfrac{a}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-2\right)^2}\)
\(=\dfrac{a+\sqrt{a}}{\sqrt{a}-2}\cdot\dfrac{\sqrt{a}-2}{\sqrt{a}+1}\cdot\dfrac{\sqrt{a}-2}{1}\)
\(=\sqrt{a}\left(\sqrt{a}-2\right)\)
\(=a-2\sqrt{a}\)
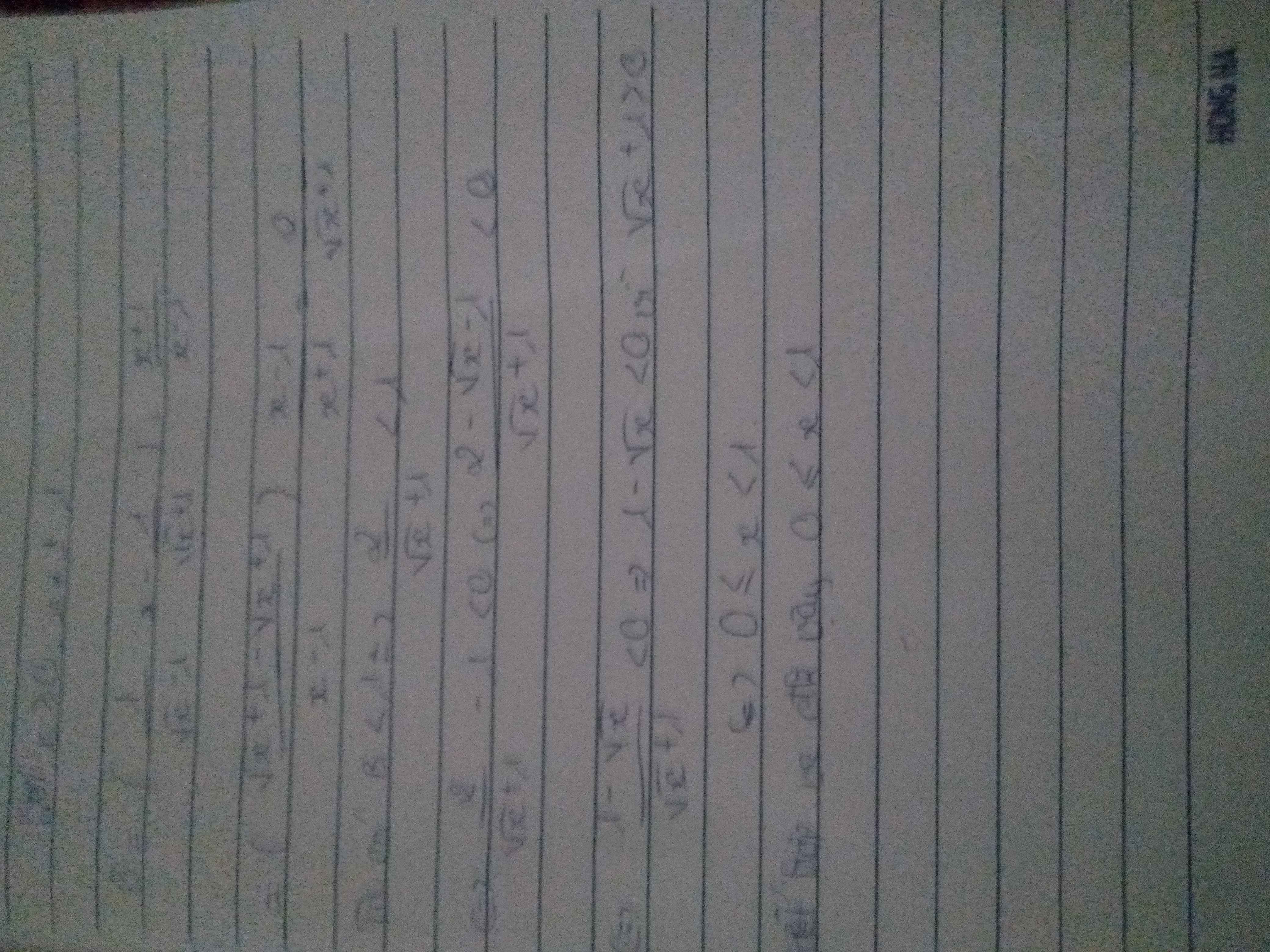
Lời giải:
\(B=\frac{3}{x-1}\sqrt{\frac{(x-1)^2}{(3x)^2}}=\frac{3}{x-1}|\frac{x-1}{3x}|\)
\(=\frac{3}{x-1}.\frac{1-x}{3x}=\frac{-1}{x}\)
\(B=\dfrac{3}{x-1}.\sqrt{\dfrac{x^2-2x+1}{9x^2}}=\dfrac{3}{x-1}.\sqrt{\left(\dfrac{x-1}{3x}\right)^2}\)
\(=\dfrac{3}{x-1}.\left|\dfrac{x-1}{3x}\right|=\dfrac{3}{x-1}.\dfrac{1-x}{3x}=-\dfrac{1}{x}\)