
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)=4xy\\ b,\left(x+y\right)^2+\left(x-y\right)^2-2\left(x+y\right)\left(x-y\right)=\left(x+y-x+y\right)^2=4y^2\\ c,\left(x^2-1\right)\left(x^2-x+1\right)\\ =\left(x-1\right)\left(x+1\right)\left(x^2-x+1\right)\\ =\left(x-1\right)\left(x^3+1\right)\\ =x^4-x^3+x-1\)
a. (x + y)2 - (x - y)2
= (x + y - x + y)(x + y + x - y)
= 2y . 2x
= 4xy
b. (x + y)2 + (x - y)2 - 2(x + y)(x - y)
= (x2 + 2xy + y2) + (x2 - 2xy + y2) - 2(x2 - y2)
= x2 + 2xy + y2 + x2 - 2xy + y2 - 2x2 + 2y2
= x2 + x2 - 2x2 + 2xy - 2xy + y2 + y2 + 2y2
= 4y2
c. (x2 - 1)(x2 - x + 1)
= x4 - x3 + x2 - x2 + x - 1
= x4 - x3 + x - 1

Lời giải:
a.
$=-2x^5+10x^4+2424x^3-x^3-3=-2x^5+10x^4+2423x^3-3$
b.
$=(x-5y)^2+2(x-5y)(x+y)+(x+y)^2$
$=[(x-5y)+(x+y)]^2=(2x-4y)^2=4x^2-16xy+16y^2$


1) \(A=\left(x+y\right)^2+4xy=x^2+2xy+y^2+4xy=x^2+6xy+y^2\)
2) \(B=\left(6x-2\right)^2+4\left(3x-1\right)\left(2+y\right)+\left(y+2\right)^2\)
\(=\left(6x-2\right)^2+2\left(6x-2\right)\left(y+2\right)+\left(y+2\right)^2\)
\(=\left(6x-2+y+2\right)^2=\left(6x+y\right)^2=36x^2+12xy+y^2\)
3) \(C=\left(x-y\right)^2+2\left(x^2-y^2\right)+\left(x+y\right)^2\)
\(=\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left(x-y+x+y\right)^2=\left(2x\right)^2=4x^2\)

B1
a, \(=>A=\left(x+y+x-y\right)\left(x+y-x+y\right)=2x.2y=4xy\)
b, \(=>B=\left[\left(x+y\right)-\left(x-y\right)\right]^2=\left[x+y-x+y\right]^2=\left[2y\right]^2=4y^2\)
c,\(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\)\(\left(x+1\right)\left(x^2-x+1\right)\left(x-1\right)\left(x^2+x+1\right)=\left(x^3+1^3\right)\left(x^3-1^3\right)=x^6-1\)
d, \(\left(a+b-c\right)^2+\left(a-b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a-b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c+b-c\right)\left(a+b-c-b+c\right)\)
\(+\left(a-b+c+b-c\right)\left(a-b+c-b+c\right)\)
\(=a\left(a+2b-2c\right)+a\left(a-2b\right)\)
\(=a\left(a+2b-2c+a-2b\right)=a\left(2a-2c\right)=2a^2-2ac\)
B2:
\(\)\(x+y=3=>\left(x+y\right)^2=9=>x^2+2xy+y^2=9\)
\(=>xy=\dfrac{9-\left(x^2+y^2\right)}{2}=\dfrac{9-\left(17\right)}{2}=-4\)
\(=>x^3+y^3=\left(x+y\right)\left(x^2-xy+y^2\right)=3\left(17+4\right)=63\)
Bài 1:
a) Ta có: \(\left(x+y\right)^2-\left(x-y\right)^2\)
\(=x^2+2xy+y^2-x^2+2xy+y^2\)
=4xy
b) Ta có: \(\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y-x+y\right)^2\)
\(=\left(2y\right)^2=4y^2\)
c) Ta có: \(\left(x^2+x+1\right)\left(x^2-x+1\right)\left(x^2-1\right)\)
\(=\left(x-1\right)\left(x^2+x+1\right)\left(x+1\right)\left(x^2-x+1\right)\)
\(=\left(x^3-1\right)\left(x^3+1\right)\)
\(=x^6-1\)
d) Ta có: \(\left(a+b-c\right)^2+\left(a+b+c\right)^2-2\left(b-c\right)^2\)
\(=\left(a+b-c\right)^2-\left(b-c\right)^2+\left(a+b+c\right)^2-\left(b-c\right)^2\)
\(=\left(a+b-c-b+c\right)\left(a+b-c+b-c\right)+\left(a+b+c-b+c\right)\left(a+b+c+b-c\right)\)
\(=a\cdot\left(a+2b-2c\right)+\left(a+2c\right)\left(a-2b\right)\)
\(=a^2+2ab-2ac+a^2-2ab+2ac-4bc\)
\(=2a^2-4bc\)

Bài 2:
a: Ta có: \(2\left(5x-8\right)-3\left(4x-5\right)=4\left(3x-4\right)+11\)
\(\Leftrightarrow10x-16-12x+15=12x-16+11\)
\(\Leftrightarrow-14x=-4\)
hay \(x=\dfrac{2}{7}\)
b: Ta có: \(2x\left(6x-2x^2\right)+3x^2\left(x-4\right)=8\)
\(\Leftrightarrow12x^2-4x^3+3x^3-12x^2=8\)
\(\Leftrightarrow x^3=-8\)
hay x=-2
Bài 1:
a: Ta có: \(I=x\left(y^2-xy^2\right)+y\left(x^2y-xy+x\right)\)
\(=xy^2-x^2y^2+x^2y^2-xy^2+xy\)
\(=xy\)
=1
b: Ta có: \(K=x^2\left(y^2+xy^2+1\right)-\left(x^3+x^2+1\right)\cdot y^2\)
\(=x^2y^2+x^3y^2+x^2-x^3y^2-x^2y^2-y^2\)
\(=x^2-y^2\)
\(=\dfrac{1}{4}-\dfrac{1}{4}=0\)

Câu 1:
\(25\left(x-y\right)^2-16\left(x+y\right)^2\)
\(=\left[5\left(x-y\right)\right]^2-\left[4\left(x+y\right)\right]^2\)
\(=\left(5x-5y\right)^2-\left(4x+4y\right)^2\)
\(=\left(5x-5y-4x-4y\right)\left(5x-5y+4x+4y\right)\)
\(=\left(x-9y\right)\left(9x-y\right)\)
Bài 2:
a: ĐKXĐ: \(x\notin\left\{1;-\dfrac{1}{2}\right\}\)
b: \(P=\left(\dfrac{1}{x-1}-\dfrac{x}{1-x^3}\cdot\dfrac{x^2+x+1}{x+1}\right):\dfrac{2x+1}{x^2+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x^2+x+1\right)}\cdot\dfrac{x^2+x+1}{x+1}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\left(\dfrac{1}{x-1}+\dfrac{x}{\left(x-1\right)\left(x+1\right)}\right)\cdot\dfrac{x^2+1}{2x+1}\)
\(=\dfrac{x+1+x}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x^2+1}{2x+1}=\dfrac{x^2+1}{x^2-1}\)
c: Thay x=1/2 vào P, ta được:
\(P=\dfrac{\left(\dfrac{1}{2}\right)^2+1}{\left(\dfrac{1}{2}\right)^2-1}=\dfrac{5}{4}:\dfrac{-3}{4}=\dfrac{5}{4}\cdot\dfrac{-4}{3}=-\dfrac{5}{3}\)

Bài 1:
a. \(=[(3x+(4y-5z)][3x-(4y-5z)]=(3x)^2-(4y-5z)^2\)
\(=9x^2-(16y^2-40yz+25z^2)=9x^2-16y^2+40yz-25z^2\)
b.
\(=(3a-1)^2+2(3a-1)(3a+1)+(3a+1)^2=[(3a-1)+(3a+1)]^2=(6a)^2=36a^2\)
Bài 2:
\((x+y+z)^3=[(x+y)+z]^3=(x+y)^3+3(x+y)^2z+3(x+y)z^2+z^3\)
\(=[x^3+y^3+3xy(x+y)]+3(x+y)z(x+y+z)+z^3\)
\(=x^3+y^3+z^3+3xy(x+y)+3(x+y)z(x+y+z)\)
\(=x^3+y^3+z^3+3(x+y)(xy+zx+zy+z^2)\)
\(=x^3+y^3+z^3+3(x+y)(z+x)(z+y)\) (đpcm)

a) \(Q=\left(x-y\right)^2-4\left(x-y\right)\left(x+2y\right)+4\left(x+2y\right)^2\)
\(Q=\left(x-y\right)^2-2\cdot\left(x-y\right)\cdot2\left(x+2y\right)+\left[2\left(x+2y\right)\right]^2\)
\(Q=\left[\left(x-y\right)-2\left(x+2y\right)\right]^2\)
\(Q=\left(x-y-2x-4y\right)^2\)
\(Q=\left(-x-5y\right)^2\)
b) \(A=\left(xy+2\right)^3-6\left(xy+2\right)^2+12\left(xy+2\right)-8\)
\(A=\left(xy+2\right)^3-3\cdot2\cdot\left(xy+2\right)^2+3\cdot2^2\cdot\left(xy+2\right)-2^3\)
\(A=\left[\left(xy+2\right)-2\right]^3\)
\(A=\left(xy+2-2\right)^3\)
\(A=\left(xy\right)^3\)
\(A=x^3y^3\)
c) \(\left(x+2\right)^3+\left(x-2\right)^3-2x\left(x^2+12\right)\)
\(=\left(x^3+6x^2+12x+8\right)+\left(x^2-6x^2+12x-8\right)-\left(2x^3+24x\right)\)
\(=x^3+6x^2+12x+8+x^2-6x^2+12x-8-2x^3-24x\)
\(=\left(x^3+x^3-2x^3\right)+\left(6x^2-6x^2\right)+\left(12x+12x-24x\right)+\left(8-8\right)\)
\(=0\)
a: =(x-y)^2-2(x-y)(2x+4y)+(2x+4y)^2
=(x-y-2x-4y)^2=(-x-5y)^2=x^2+10xy+25y^2
b: =(xy+2-2)^3=(xy)^3=x^3y^3
c: =x^3+6x^2+12x+8+x^3-6x^2+12x-8-2x(x^2+12)
=24x+2x^3-2x^3-24x
=0
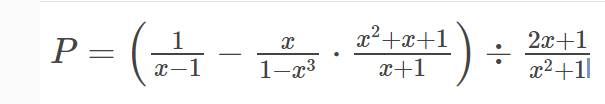
a, \(\left(x+y\right)^2+\left(x-y\right)^2=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2\)
b, \(\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2=\left(x-y+x+y\right)^2=4x^2\)
a) \(\left(x+y\right)^2+\left(x-y\right)^2\)
\(=x^2+2xy+y^2+x^2-2xy+y^2=2x^2+2y^2\)
b) \(2\left(x-y\right)\left(x+y\right)+\left(x-y\right)^2+\left(x+y\right)^2\)
\(=\left(x-y\right)^2+2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2\)
\(=\left[\left(x-y\right)^2+\left(x+y\right)^2\right]\)
\(=\left(x-y+x+y\right)^2=\left(2x\right)^2=4x^2\)