BQ
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) 2x(x+3) – 3x2(x+2) + x(3x2 + 4x – 6)
= (2x . x + 2x . 3) – (3x2 . x + 3x2 . 2) + (x . 3x2 + x . 4x – x . 6)
= 2x2 + 6x – (3x3 + 6x2) + (3x3 + 4x2 - 6x)
= 2x2 + 6x – 3x3 – 6x2 + 3x3 + 4x2 - 6x
= (– 3x3 + 3x3 ) + (2x2 - 6x2 + 4x2 ) + (6x – 6x)
= 0 + 0 + 0
= 0
b) 3x(2x2 – x) – 2x2(3x+1) + 5(x2 – 1)
= [3x . 2x2 + 3x . (-x)] – (2x2 . 3x + 2x2 . 1) + [5x2 + 5 . (-1)]
= 6x3 – 3x2 – (6x3 +2x2) + 5x2 – 5
= 6x3 – 3x2 – 6x3 - 2x2 + 5x2 – 5
= (6x3 – 6x3 ) + (-3x2 – 2x2 + 5x2) – 5
= 0 + 0 – 5
= - 5
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) 4x2(5x2 + 3) – 6x(3x3 – 2x + 1) – 5x3 (2x – 1)
= 4x2 . 5x2 + 4x2 . 3 – [6x . 3x3 + 6x . (-2x) + 6x . 1] – [5x3 . 2x + 5x3 . (-1)]
= 20x4 + 12x2 – (18x4 – 12x2 + 6x) – (10x4 – 5x3)
= 20x4 + 12x2 - 18x4 + 12x2 - 6x - 10x4 + 5x3
= (20x4 – 18x4 - 10x4 ) + 5x3 + (12x2 + 12x2 ) – 6x
= -8x4 + 5x3 + 24x2 – 6x
\(\begin{array}{l}b)\dfrac{3}{2}x\left( {{x^2} - \dfrac{2}{3}x + 2} \right) - \dfrac{5}{3}{x^2}(x + \dfrac{6}{5})\\ = \dfrac{3}{2}x.{x^2} + \dfrac{3}{2}x.( - \dfrac{2}{3}x) + \dfrac{3}{2}x.2 - (\dfrac{5}{3}{x^2}.x + \dfrac{5}{3}{x^2}.\dfrac{6}{5})\\ = \dfrac{3}{2}{x^3} - {x^2} + 3x - (\dfrac{5}{3}{x^3} + 2{x^2})\\ = \dfrac{3}{2}{x^3} - {x^2} + 3x - \dfrac{5}{3}{x^3} - 2{x^2}\\ = (\dfrac{3}{2}{x^3} - \dfrac{5}{3}{x^3}) + ( - {x^2} - 2{x^2}) + 3x\\ = \dfrac{{ - 1}}{6}{x^3} - 3{x^2} + 3x\end{array}\)
HN
3
H9
HT.Phong (9A5)
CTVHS
27 tháng 6 2023
Bài 1:
a) \(3x^2\left(2x^3-x+5\right)-6x^5-3x^3+10x^2\)
\(=6x^5-3x^3+10x^2-6x^5-3x^3+10x^2\)
\(=10x^2+10x^2\)
\(=20x^2\)
b) \(-2x\left(x^3-3x^2-x+11\right)-2x^4+3x^3+2x^2-22x\)
\(=-2x^4+6x^3+2x^2-22x-2x^4+3x^3+2x^2-22x\)
\(=-4x^4+9x^3+4x^2-44x\)
HQ
Hà Quang Minh
Giáo viên
20 tháng 9 2023
a) Cách 1:
\(6(y - x) - 2(x - y)\)
\( = 6y - 6x - 2x + 2y\)
\( = 8y - 8x\)
Cách 2:
\(6(y - x) - 2(x - y)\\= 6(y-x)+2(y-x)\\=(6+2).(y-x)\\=8.(y-x)\\=8y-8x\)
b) \(3{x^2} + x - 4x - 5{x^2}\)
\( = (3{x^2} - 5{x^2}) + (x - 4x)\)
\( = - 2{x^2} - 3x\)
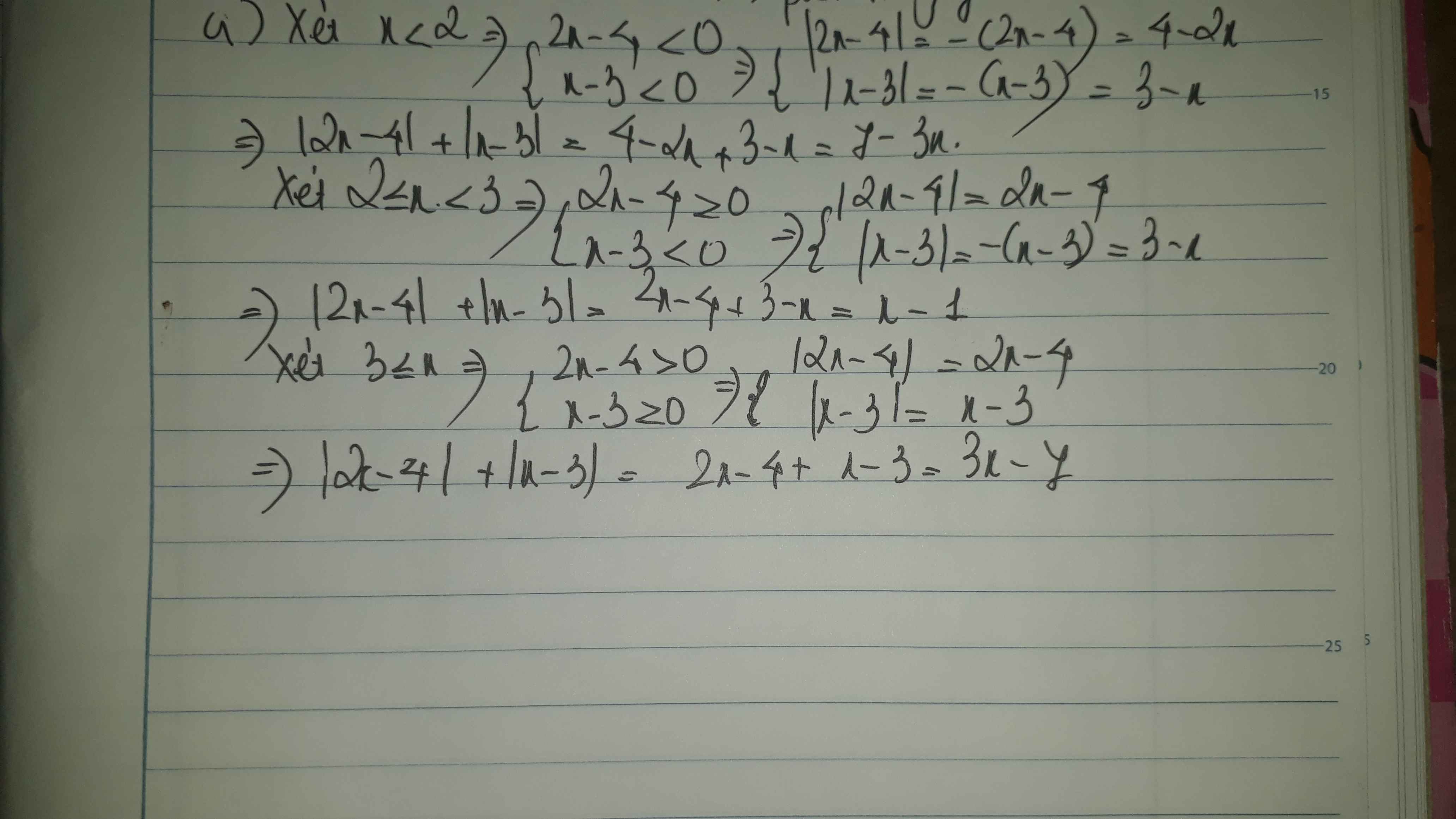
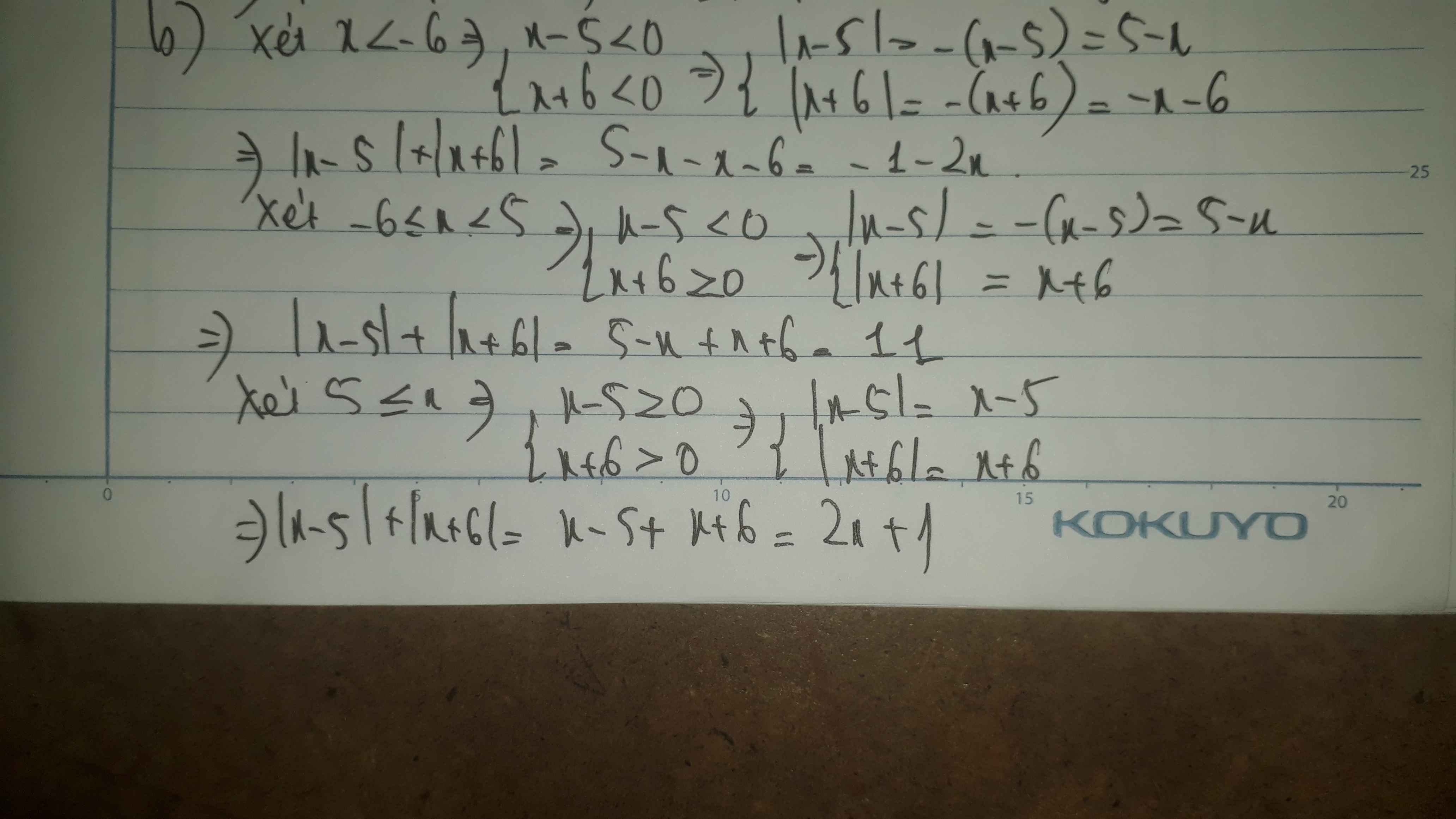
A=3.(2x-1) - Ix-5I
a)xét 2 trường hợp:
TH(1) : A=6x-3-x+5 (x-5>=0) = 5x-2
TH(2) : A=6x-3-5+x (x-5<0) = 7x-8
Câu nào đúng z