
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




với x \(\ge\)-3 thì x+ 3 \(\ge\)0 nên |x+3|= x+3
khi đó A = 3x -1 - 2 ( x + 3 ) = x - 7
với x < -3 thì x + 3 < 0 nên |x+3| = -x-3
khi đó A = 3x - 1 - 2 ( -x - 3 ) = 5x + 5

Ta có:\(\frac{\left[x\left(x-2\right)\right]}{x^2+8x-20}+12x-3=\frac{x\left(x-2\right)}{x^2-2x+10x-20}+12x-3\)
\(=\frac{x\left(x-2\right)}{x\left(x-2\right)+10\left(x-2\right)}+12x-3=\frac{x\left(x-2\right)}{\left(x+10\right)\left(x-2\right)}+12x-3\)
\(=\frac{x}{x+10}+12x-3=\frac{x+\left(12x-3\right).\left(x+10\right)}{x+10}=\frac{x+12x^2+120x-3x-30}{x+10}\)
\(=\frac{12x^2+118x-30}{x+10}\)

1)10x-3x(x-5)+3(x2-4x)-3x
<=>3(x2-4x)+10x-3x-3x(x-5)
<=>3(x2-4x)=7x-3x(x-5)
<=>3x2-12x+7x-3x2+15x
<=>3x2-3x2-12x+7x+15x
<=>-12x+7x+15x
<=>10x
2)5y+1-4.5y
<=>51.5y-4.5y
<=>5y(51-4)
<=>5y.1
<=>5y


\(Bài.44:\\ a,3x-7=0\\ \Leftrightarrow3x=7\\ \Leftrightarrow x=\dfrac{7}{3}\\ b.2x^2+9=0\\ \Leftrightarrow x^2=-\dfrac{9}{2}\left(vô.lí\right)\\ \Rightarrow Không.có.x.thoả.mãn\)
43:
a: \(A=2x\left(x^2-2x-3\right)-6x^2+5x-1+9x^2+3x+3\)
\(=2x^3-4x^2-6x+3x^2+8x+2\)
\(=2x^3-x^2+2x+2\)
b: \(\dfrac{A}{2x-1}=\dfrac{x^2\left(2x-1\right)+2x-1+3}{2x-1}=x^2+1+\dfrac{3}{2x-1}\)
Thương là x^2+1
Dư là 3
c: A chia hết cho 2x-1
=>3 chia hết cho 2x-1
=>2x-1 thuộc {1;-1;3;-3}
=>x thuộc {1;0;2;-1}
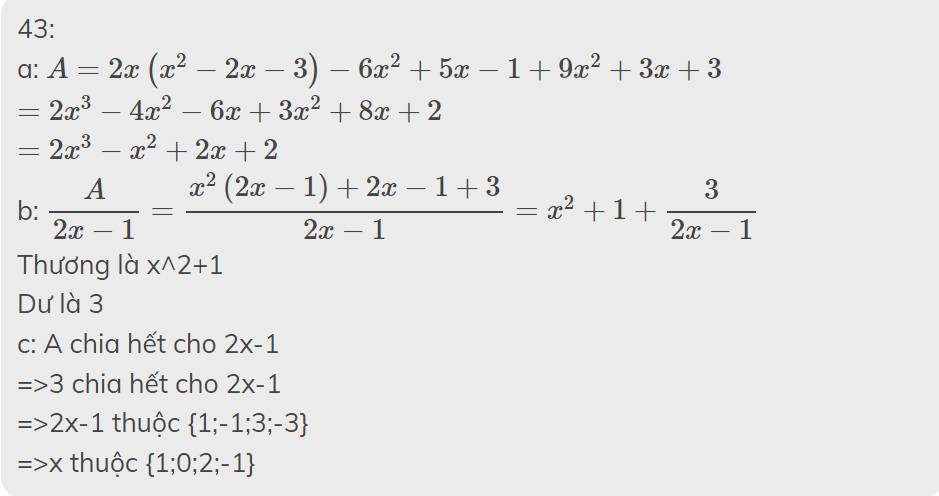
9x - 7i > 3 . \((3x-7u)\)
=> 9x - 71 > 9x - 21u
=> -7i > -21u
=> 7i < 21u
=> i < 3u
9x - 7i > 3 (3x - 7u)
9x-7i>9x-21u
-7i>-21u
i<3u