ND
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AT
7 tháng 7 2021
\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{5}{\sqrt{5}}\right)\left(\sqrt{5}-\sqrt{2}\right)=\left(\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}-\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)\)
\(=\left(-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)=-\left(\sqrt{2}+\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)=-3\)
TG
7 tháng 7 2021
\(=\left[\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{1-\sqrt{3}}-\sqrt{5}\right]\left(\sqrt{5}-\sqrt{2}\right)=\left(-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{5}-\sqrt{2}\right)=-\left(\sqrt{5}+\sqrt{2}\right)\left(\sqrt{5}-\sqrt{2}\right)=-3\)
4 tháng 7 2017
được bạn ạ mình nhờ thầy giải ra mà bạn tính máy tính mới ko ra thôi
23 tháng 7 2021
d) Ta có: \(D=\left(\dfrac{5\sqrt{x}-6}{x-9}-\dfrac{2}{\sqrt{x}+3}\right):\left(1+\dfrac{6}{x-9}\right)\)
\(=\dfrac{5\sqrt{x}-6-2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}:\dfrac{x-9+6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{5\sqrt{x}-6-2\sqrt{x}+6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{x-3}\)
\(=\dfrac{3\sqrt{x}}{x-3}\)
f) Ta có: \(\left(\dfrac{3}{\sqrt{1+x}}+\sqrt{1-x}\right):\left(\dfrac{3}{\sqrt{1-x^2}}+1\right)\)
\(=\dfrac{3+\sqrt{1-x^2}}{\sqrt{1+x}}:\dfrac{3+\sqrt{1-x^2}}{\sqrt{1-x^2}}\)
\(=\dfrac{\sqrt{1-x^2}}{\sqrt{1+x}}=\sqrt{1-x}\)
5 tháng 5 2021
Câu 1:
Sửa đề: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
Ta có: \(B=\left(\dfrac{x}{x+3\sqrt{x}}+\dfrac{1}{\sqrt{x}+3}\right):\left(1-\dfrac{2}{\sqrt{x}}+\dfrac{6}{x+3\sqrt{x}}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}+3\right)}+\dfrac{1}{\sqrt{x}+3}\right):\left(\dfrac{x+3\sqrt{x}-2\left(\sqrt{x}+3\right)+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\right)\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}:\dfrac{x+3\sqrt{x}-2\sqrt{x}-6+6}{\sqrt{x}\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}+3}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{x+\sqrt{x}}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=1\)
5 tháng 5 2021
Câu 3:
Ta có: \(Q=\left(\dfrac{a}{a-2\sqrt{a}}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{a-4\sqrt{a}+4}\)
\(=\left(\dfrac{a}{\sqrt{a}\left(\sqrt{a}-2\right)}+\dfrac{a}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}+1}{\left(\sqrt{a}-2\right)^2}\)
\(=\dfrac{a+\sqrt{a}}{\sqrt{a}-2}\cdot\dfrac{\sqrt{a}-2}{\sqrt{a}+1}\cdot\dfrac{\sqrt{a}-2}{1}\)
\(=\sqrt{a}\left(\sqrt{a}-2\right)\)
\(=a-2\sqrt{a}\)
29 tháng 7 2018
\(\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{3}-2\right)\left(\sqrt{2+\sqrt{3}}\right)=\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{3}-2\right)\left(\frac{\sqrt{6}+\sqrt{2}}{2}\right)\)\(=\left(2+\sqrt{3}\right)\left(\sqrt{3}-2\right)=-1\)
KT
29 tháng 7 2018
\(\left(\sqrt{6}+\sqrt{2}\right)\left(\sqrt{3}-2\right).\sqrt{2+\sqrt{3}}\)
\(=\sqrt{2}.\left(\sqrt{3}+1\right)\left(\sqrt{3}-2\right).\sqrt{2+\sqrt{3}}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-2\right).\sqrt{4+2\sqrt{3}}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-2\right).\sqrt{\left(\sqrt{3}+1\right)^2}\)
\(=\left(\sqrt{3}+1\right)\left(\sqrt{3}-2\right)\left(\sqrt{3}+1\right)\)
\(=\left(\sqrt{3}+1\right)^2\left(\sqrt{3}-2\right)\)
\(=\left(4+2\sqrt{3}\right)\left(\sqrt{3}-2\right)\)
\(=2\left(2+\sqrt{3}\right)\left(\sqrt{3}-2\right)\)
\(=-2\)
NT
1
9 tháng 8 2015
\(\sqrt{2}D=\left(3\sqrt{2}+\sqrt{6}\right)\cdot\sqrt{12-6\sqrt{3}}=\left(3\sqrt{2}+\sqrt{6}\right)\sqrt{9-2.3\sqrt{3}+3}\)
\(\left(3\sqrt{2}+\sqrt{6}\right)\left(3-\sqrt{3}\right)\)
Nhân ra rút gọn
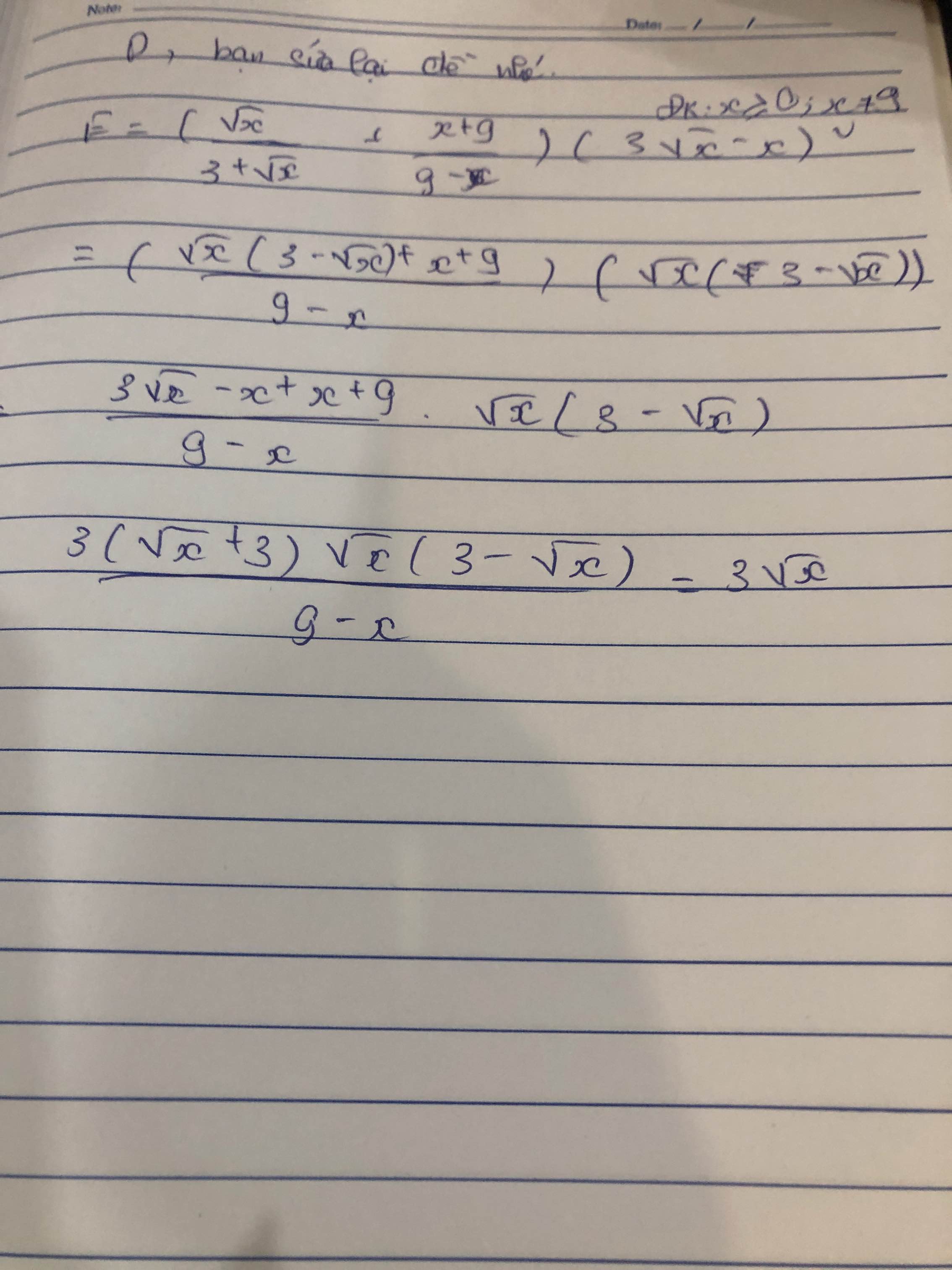
\(\left(3\sqrt{2}+\sqrt{6}\right)\sqrt{6-3\sqrt{3}}=\left(3+\sqrt{3}\right)\sqrt{12-6\sqrt{3}}=\left(3+\sqrt{3}\right)\sqrt{9-2.3.\sqrt{3}+3}\)
\(=\left(3+\sqrt{3}\right)\sqrt{3^2-2.3.\sqrt{3}+\left(\sqrt{3}\right)^2}=\left(3+\sqrt{3}\right)\sqrt{\left(3-\sqrt{3}\right)^2}\)
\(=\left(3+\sqrt{3}\right)\left|3-\sqrt{3}\right|=\left(3+\sqrt{3}\right)\left(3-\sqrt{3}\right)=6\)