
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)

Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.

a) \(A=\left(\sqrt{x}+3\right)^2-4\sqrt{x}-6\)
\(A=x+6\sqrt{x}+9-4\sqrt{x}-6\)
\(A=x+2\sqrt{x}-3\)
b) \(A=x+2\sqrt{x}-3\)
\(A=x+3\sqrt{x}-\sqrt{x}-3\)
\(A=\sqrt{x}\left(\sqrt{x}+3\right)-\left(\sqrt{x}+3\right)\)
\(A=\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)\)
a: A=x+6căn x+9-4căn x-6
=x+2căn x+3
b: A ko phân tích được nha bạn

a ) 2 - 3 2 = 2 - 3 = 2 - 3
(vì 2 - √3 > 0 do 2 = √4 mà √4 > √3)
b ) 3 - 11 2 = 3 - 11 = 11 - 3
(vì √11 - 3 > 0 do 3 = √9 mà √11 > √9)
c) 2√a2 = 2|a| = 2a với a ≥ 0
d ) 3 a - 2 2 = 3 a - 2 = 3 2 - a
(vì a < 2 nên 2 – a > 0)

1) \(A=3\sqrt{\dfrac{1}{3}}-\dfrac{5}{2}\sqrt{12}-\sqrt{48}\)
\(=3\cdot\dfrac{\sqrt{1}}{\sqrt{3}}-\dfrac{5\sqrt{12}}{2}-\sqrt{4^2\cdot3}\)
\(=\dfrac{3\cdot1}{\sqrt{3}}-\dfrac{5\cdot2\sqrt{3}}{2}-4\sqrt{3}\)
\(=\sqrt{3}-5\sqrt{3}-4\sqrt{3}\)
\(=-8\sqrt{3}\)
2) \(A=\sqrt{12-4x}\) có nghĩa khi:
\(12-4x\ge0\)
\(\Leftrightarrow4x\le12\)
\(\Leftrightarrow x\le\dfrac{12}{4}\)
\(\Leftrightarrow x\le3\)
3) \(\dfrac{2x-2\sqrt{x}}{x-1}\)
\(=\dfrac{2\sqrt{x}\cdot\sqrt{x}-2\sqrt{x}}{\left(\sqrt{x}\right)^2-1^2}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{\text{x}}}{\sqrt{x}+1}\)
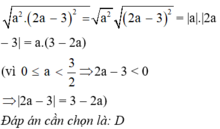
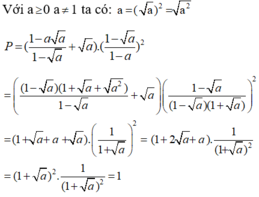

 (Với x > 0; x 1; x4)
(Với x > 0; x 1; x4)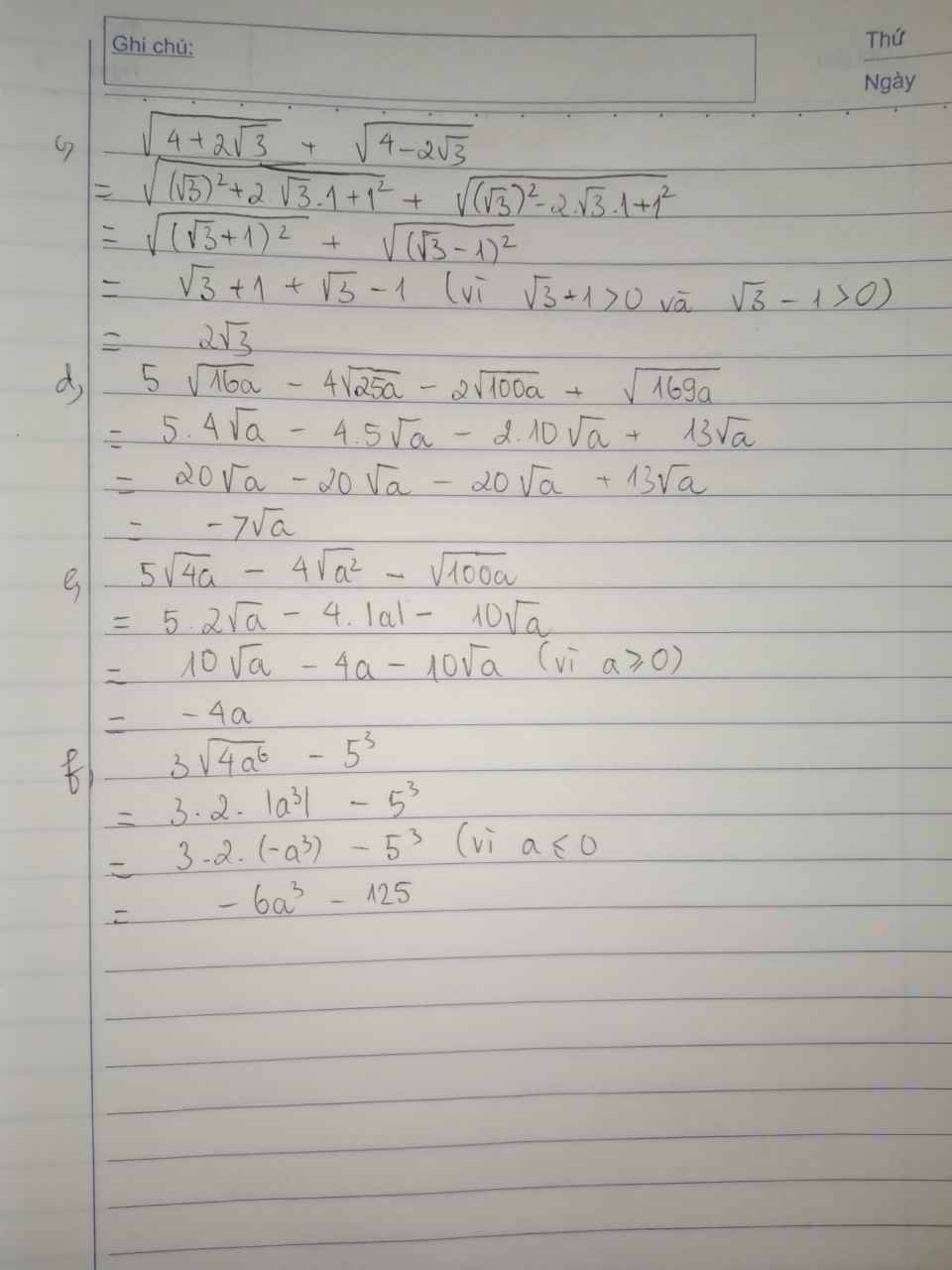
\(2\sqrt{a^2}=2\left|a\right|=2a\) (với \(a\ge0\) )
\(3\sqrt{\left(a-2\right)^2}=3\left|a-2\right|=3\left(2-a\right)=6-3a\) (\(a< 2\))
a: \(2\sqrt{a^2}=-2a\)
b: \(3\sqrt{\left(a-2\right)^2}=3\left|a-2\right|=3\left(2-a\right)\)