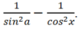K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
12 tháng 9 2019
Chọn C.
Ta có: cota + tana) 2 = cot2a + 2.cota.tana + tan2a
= (cot2a + 1) + (tan2a + 1)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 6 2020
\(-\frac{\pi}{2}< a< 0\Rightarrow cosa>0\)
\(\Rightarrow cosa=\sqrt{1-sin^2a}=\frac{4}{5}\)
\(tana=\frac{sina}{cosa}=-\frac{3}{4}\)
\(A=\frac{tana+cota}{1+tan^2a}=\frac{tana+\frac{1}{tana}}{1+tan^2a}=\frac{1+tan^2a}{\left(1+tan^2a\right)tana}=\frac{1}{tana}=cota\)
TN
0
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
\(sina=\frac{3}{5}\Rightarrow sin^2a=\frac{9}{25}\) ; \(cos^2a=1-\frac{9}{25}=\frac{16}{25}\)
\(A=\frac{cota+tana}{cota-tana}=\frac{sina.cosa\left(cota+tana\right)}{sina.cosa\left(cota-tana\right)}=\frac{cos^2a+sin^2a}{cos^2a-sin^2a}=\frac{1}{cos^2a-sin^2a}=\frac{1}{\frac{16}{25}-\frac{9}{25}}=\frac{25}{7}\)
\(B=\frac{sin^2a-cos^2a}{sin^2a-3cos^2a}=\frac{\frac{sin^2a}{sin^2a}-\frac{cos^2a}{sin^2a}}{\frac{sin^2a}{sin^2a}-\frac{3cos^2a}{sin^2a}}=\frac{1-cot^2a}{1-3cot^2a}=\frac{1-\left(-\frac{1}{3}\right)^2}{1-3\left(-\frac{1}{3}\right)^2}=\)
\(C_1=sin^2a+cos^2a+cos^2a=1+cos^2a=1+\frac{1}{1+tan^2a}=1+\frac{1}{1+\left(-2\right)^2}\)
\(C_2=\left(sin^2a+cos^2a\right)\left(sin^2a-cos^2a\right)=sin^2a-cos^2a=1-2cos^2a\)
\(=1-\frac{2}{1+tan^2a}=1-\frac{2}{1+\left(-2\right)^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2020
\(A=\frac{1-sinx-1+2sin^2x}{2sinx.cosx-cosx}=\frac{sinx\left(2sinx-1\right)}{cosx\left(2sinx-1\right)}=\frac{sinx}{cosx}=tanx\)
\(B=\frac{2sinx.cosx+sinx}{1+2cos^2x-1+cosx}=\frac{sinx\left(2cosx+1\right)}{cosx\left(2cosx+1\right)}=\frac{sinx}{cosx}=tanx\)
\(C=\frac{sina.cosa\left(tana-cota\right)}{sina.cosa\left(tana+cota\right)}+cos2a=\frac{sin^2a-cos^2a}{sin^2a+cos^2a}+cos2a\)
\(=-cos2a+cos2a=0\)
Q
1
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 5 2020
\(\left(cota+tana\right)^2-\left(cota-tana\right)^2\)
\(=cot^2a+tan^2a+2tana.cota-cot^2a-tan^2a+2tana.cota\)
\(=4tana.cota=4\)