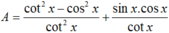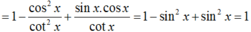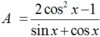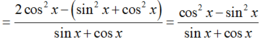K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
8 tháng 1 2019
Đáp án: A
Ta có:
A = c o s 2 x + sin 2 x + sin 2 x 2 sin x + c o s x
PT
1
CM
20 tháng 6 2018
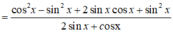
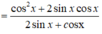
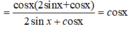
Chọn D.
Với 2 góc phụ nhau thì sin góc này bằng cos góc kia và ngược lại . do đó ta có:
A = cos540.cos 40 – cos360.cos860 = cos540.cos 40 – sin 540.sin40
= cos ( 540 + 40) = cos 580
CM
7 tháng 4 2019
Chọn C.
Ta có A = sin 2a.tan2a + 4sin2a - tan2a + 3cos2a
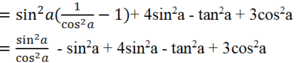
= 3sin2a + 3cos2a = 3.
PT
1
DM
2
2
6 tháng 5 2022
`A=[sin x + sin 2x + sin 3x]/[cos x + cos 2x + cos 3x]`
`A=[2sin2x.cosx+sin2x]/[2cos2x.cosx+cos2x]`
`A=[sin2x(2cosx+1)]/[cos2x(2cosx+1)]`
`A=tan 2x`
6 tháng 5 2022
\(A=\dfrac{sinx-sin2x+sin3x}{cosx-cos2x+cos3x}\)
\(ĐK\left\{{}\begin{matrix}cos2x\ne0\\cosx\ne\dfrac{1}{2}\end{matrix}\right.\) \(\Leftrightarrow\) \(A=\dfrac{sinx+sin3x-sin2x}{cosx+cos3x-cos2x}\)
\(\Leftrightarrow\) \(\left\{{}\begin{matrix}=\dfrac{2sin2x.cosx-sin2x}{2cos2x.cosx-cos2x}\\=\dfrac{sin2x\left(2cosx-1\right)}{cos2x\left(2cosx-1\right)}\end{matrix}\right.\) \(\Rightarrow\) \(A=tan2x\)