Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) (a+b)3+(a-b)3=a3+3a2b+3ab2+b3+a3-3a2b+3ab2-b3
=2a3+6ab2
b) (a + b + c)2 + (a − b − c)2 + (b − c − a)2 + (c − a − b)2
=a2+b2+c2+2ab+2bc+2ca+a2+b2+c2-2ab+2bc-2ac+a2+b2+c2-2bc+2ca-2ba+a2+b2+c2-2ca+2ab-2cb
=4a2+4b2+4c2
a) Ta có: \(\left(a+b\right)^3+\left(a-b\right)^3\)
\(=\left(a+b+a-b\right)\left[\left(a+b\right)^2-\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]\)
\(=2a\cdot\left(a^2+2ab+b^2-a^2+b^2+a^2-2ab+b^2\right)\)
\(=2a\cdot\left(a^2+3b^2\right)\)
\(=2a^3+6ab^2\)

Sửa đề cho dễ đọc
\(1P=\frac{a^3+b^3+c^3-3abc}{a^2+b^2+c^2-ab-bc-ca}\)
\(\Leftrightarrow1P=\frac{\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)}{a^2+b^2+c^2-ab-bc-ca}=a+b+c\)

Áp dụng hằng đẳng thức dưới dạng
\(x^3+y^3=\left(x+y\right)^3-3xy\left(x+y\right)\)
\(\left(a+b+c\right)^3+\left(a-b-c\right)^3=\left(2a\right)^3-3\left(a+b+c\right)\left(a-b-c\right).2a\)
\(\left(b-c-a\right)^3+\left(c-a-b\right)^3=\left(-2a\right)^3-3\left(b-c-a\right)\left(c-a-b\right).\left(-2a\right)\)
\(\Rightarrow\left(a+b+c\right)^3+\left(a-b-c\right)^3+\left(b-c-a\right)^3+\left(c-a-b\right)^3\)
\(=\left(2\right)^3+\left(-2a\right)^3-6a\left[a+\left(b+c\right)\right]\left[a-\left(b+c\right)\right]+6a\left[-a+\left(b-c\right)\right]\left[-a-\left(b-c\right)\right]\)
\(=-6a\left\{a^2-\left(b+c\right)^2-\left[\left(-a\right)^2-\left(b-c\right)^2\right]\right\}\)
\(=-6a\left\{a^2-a^2+\left(b-c\right)^2-\left(b+c\right)^2\right\}\)
\(=-6a\left[b-c+b+c\right]\left[b-c-\left(b+c\right)\right]=-6a.2b.\left(-2c\right)\)
\(=24abc\)

Ta có:\(\left(a-b+c\right)^2+\left(a-b+c\right)^2-2\left(b-c\right)^2\)
\(=2\left(a-b+c\right)^2-2\left(b-c\right)^2\\ =2\left(\left(a-b+c\right)^2-\left(b-c\right)^2\right)\)
\(=2\left(a-b+c-b+c\right)\left(a-b+c+b-c\right)\\ =2\left(a-2b+2c\right)a \)
\(=2a^2-4ab+4ac\)

a,Đặt a+b-c=x, c+a-b=y, b+c-a=z
=>x+y+z=a+b-c+c+a-b+b+c-a=a+b+c
Ta có hằng đẳng thức:
(x+y+z)^3-3x-3y-3z=3(x+y)(x+z)(y+z)
=>(a+b+c)^3-(b+c-a)^3-(a+c-b)^3-(a+b-c)^3=(x+y+z)^3-x^3-y^3-z^3
=3(x+y)(x+z)(y+z)
=3(a+b-c+c+a-b)(c+a-b+b+c-a)(b+c-a+a+b-c)
=3.2a.2b.2c
=24abc
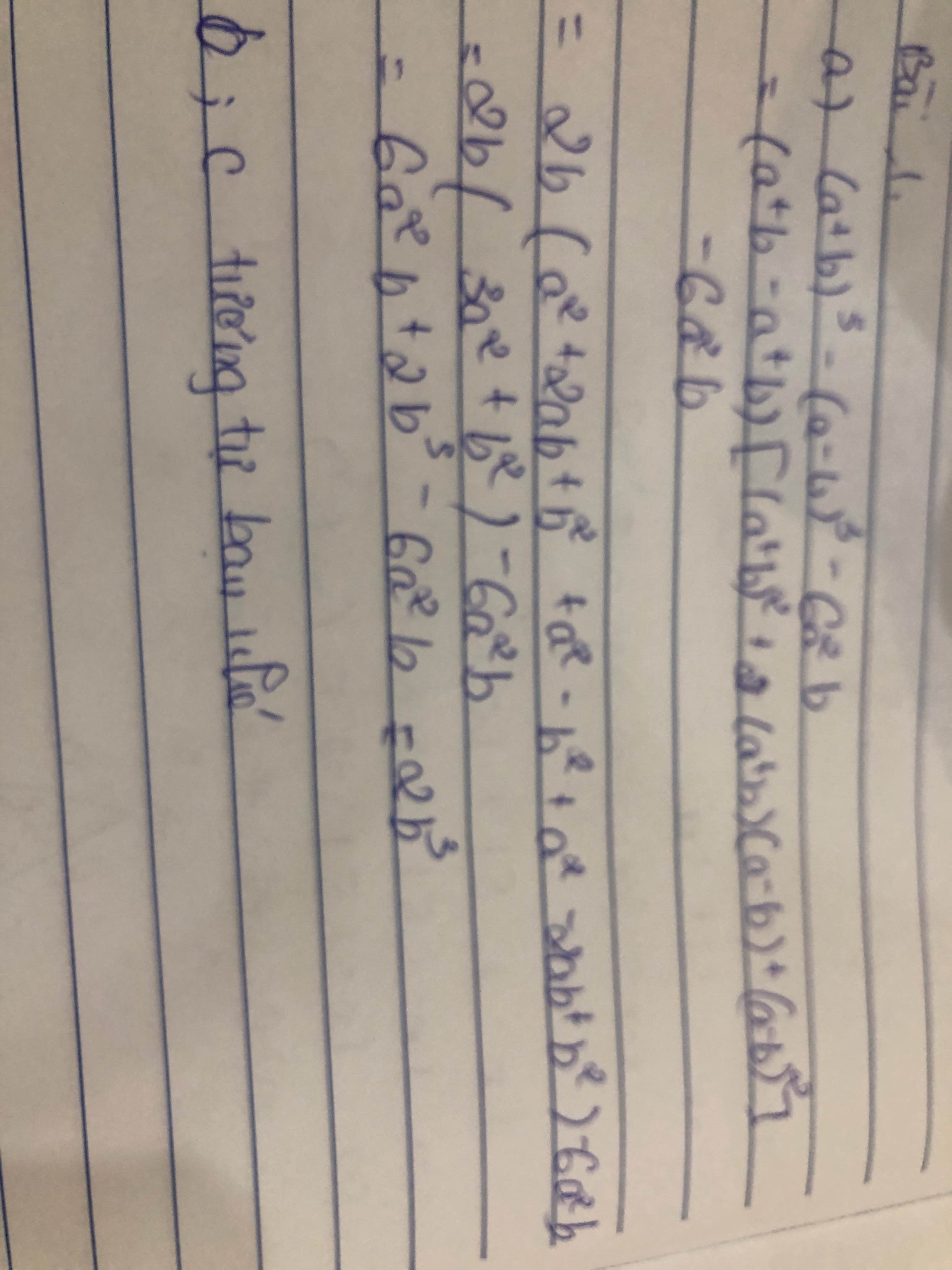
\(\left(a+b\right)^3+\left(b+c\right)^3+\left(c+a\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
Đặt \(\hept{\begin{cases}a+b=x\\b+c=y\\c+a=z\end{cases}}\)
\(\Rightarrow\left(a+b\right)^3+\left(b+c\right)^3+\left(c+a\right)^3-3\left(a+b\right)\left(b+c\right)\left(c+a\right)\)
\(=x^3+y^3+z^3-3xyz\)
\(=x^3+3x^2y+3xy^2+y^3+z^3-3x^2y-3xy^2-3xyz\)
\(=\left(x+y\right)^3+z^3-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left[\left(x+y\right)^2-\left(x+y\right).z+z^2\right]-3xy\left(x+y+z\right)\)
\(=\left(x+y+z\right)\left(x^2+2xy+y^2-xz-yz+z^2-3xy\right)\)
\(=\left(x+y+z\right)\left(x^2+y^2-xz-yz+z^2-xy\right)\)
\(=\left[\left(a+b\right)+\left(b+c\right)+\left(c+a\right)\right]\left(x^2+y^2+z^2-xy-yz-zx\right)\)
\(=2.\left(a+b+c\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\)
\(=\left(a+b+c\right)\left(2x^2+2y^2+2z^2-2xy-2yz-2zx\right)\)
\(=\left(a+b+c\right)\left[\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2zx+x^2\right)\right]\)
\(=\left(a+b+c\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\)
\(=\left(a+b+c\right)\left[\left(a+b-b-c\right)+\left(b+c-c-a\right)+\left(c+a-a-b\right)\right]\)
\(=\left(a+b+c\right)\left(a-c+b-a+c-b\right)\)
\(=\left(a+b+c\right).0\)
\(=0\)
Châu off rồi
Tham khảo nhé~
Cảm ơn bn kudo Shinichi, đây là bài tập nâng cao chuyên đề có đáp án. Mk xem đáp án rồi, là 2 ( a 3 + b 3 + c 3 - 3abc ) cơ. Còn cách lm ntn thì mk mới hỏi mn chứ. Dù sao cx cảm ơn bn đã giải bài tập giùm mk, cách của bn mk sẽ tham khảo để sử dụng vào những bài tập khác.