
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. ĐK \(x\ge0\)và \(x\ne1\)
A =\(\left(\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{\sqrt{x}}{\sqrt{x}+1}+\frac{\sqrt{x}}{1-\sqrt{x}}\right):\left(\frac{\sqrt{x}+1}{\sqrt{x}-1}+\frac{1-\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\frac{\left(\sqrt{x}+1\right)^2+\sqrt{x}\left(\sqrt{x}-1\right)-\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}:\frac{\cdot\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)\left(1-\sqrt{x}\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\frac{x+2\sqrt{x}+1+x-\sqrt{x}-x-\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}.\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{x+2\sqrt{x}+1+\sqrt{x}-x-1+\sqrt{x}}\)
\(=\frac{x+1}{4\sqrt{x}}\)
b. Thay \(x=\frac{2-\sqrt{3}}{2}\Rightarrow A=\frac{\frac{2-\sqrt{3}}{2}+1}{4\sqrt{\frac{2-\sqrt{3}}{2}}}=\frac{4-\sqrt{3}}{4\left(\sqrt{3}-1\right)}=\frac{4-\sqrt{3}}{4-4\sqrt{3}}=-\frac{1+3\sqrt{3}}{8}\)
c . Ta có \(A-\frac{1}{2}=\frac{x+1}{4\sqrt{x}}-\frac{1}{2}=\frac{x-2\sqrt{x}+1}{4\sqrt{x}}=\frac{\left(\sqrt{x}-1\right)^2}{4\sqrt{x}}>0\)với \(\forall x>0\)và \(x\ne1\)
Vậy A >1/2

\(\frac{1}{3}\sqrt{9+6a+a^2}+\frac{4a}{3}+5\)
\(=\frac{1}{3}\sqrt{\left(a+3\right)^2}+\frac{4a}{3}+5\)
\(=\frac{1}{3}\left|a+3\right|+\frac{4a}{3}+5\)(1)
Với a < 3 \(\left(1\right)=-\frac{1}{3}\left(a+3\right)+\frac{4}{3}a+5=a+4\)
Với a >= 3 \(\left(1\right)=\frac{1}{3}\left(a+3\right)+\frac{4}{3}a+5=\frac{5}{3}a+6\)

Đặt \(a=\sqrt{x+3}\) , \(b=\sqrt{x-3}\).
Ta có : \(A=\frac{\left(x+3\right)+2\sqrt{\left(x-3\right)\left(x+3\right)}}{2\left(x-3\right)+\sqrt{\left(x-3\right)\left(x+3\right)}}=\frac{a^2+2ab}{2b^2+ab}\)
\(=\frac{a^2+2ab}{2b^2+ab}=\frac{a\left(a+2b\right)}{b\left(a+2b\right)}=\frac{a}{b}=\frac{\sqrt{x+3}}{\sqrt{x-3}}\)

a) \(\sqrt{\left(\sqrt{2}-1\right)^2}-\sqrt{11+6\sqrt{2}}\)
\(=\sqrt{2}-1-3-\sqrt{2}\)
=-4
b) \(\sqrt{\left(1-\sqrt{5}\right)^2}+\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{5}-1+3-\sqrt{5}\)
=2
c) \(\sqrt{21-12\sqrt{3}}-\sqrt{13-4\sqrt{3}}\)
\(=2\sqrt{3}-3-2\sqrt{3}+1\)
=-2

Bạn xem có nhầm đề bài không phải là\(\frac{\sqrt{3}}{\sqrt{\sqrt{3}+1}-1}\) thế mới sử dụng đc trục căn thức ở mẫu

a) \(A=\sqrt{9a}-\sqrt{16a}-\sqrt{49a}=3\sqrt{a}-4\sqrt{a}-7\sqrt{a}=-8\sqrt{a}\)
b) \(B=\dfrac{3+2\sqrt{3}}{\sqrt{3}}+\dfrac{2+\sqrt{2}}{\sqrt{2}}-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=\dfrac{\sqrt{3}\left(2+\sqrt{3}\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}}-\left(\sqrt{3}+\sqrt{2}\right)\)
\(=2+\sqrt{3}+\sqrt{2}+1-\sqrt{3}-\sqrt{2}=3\)
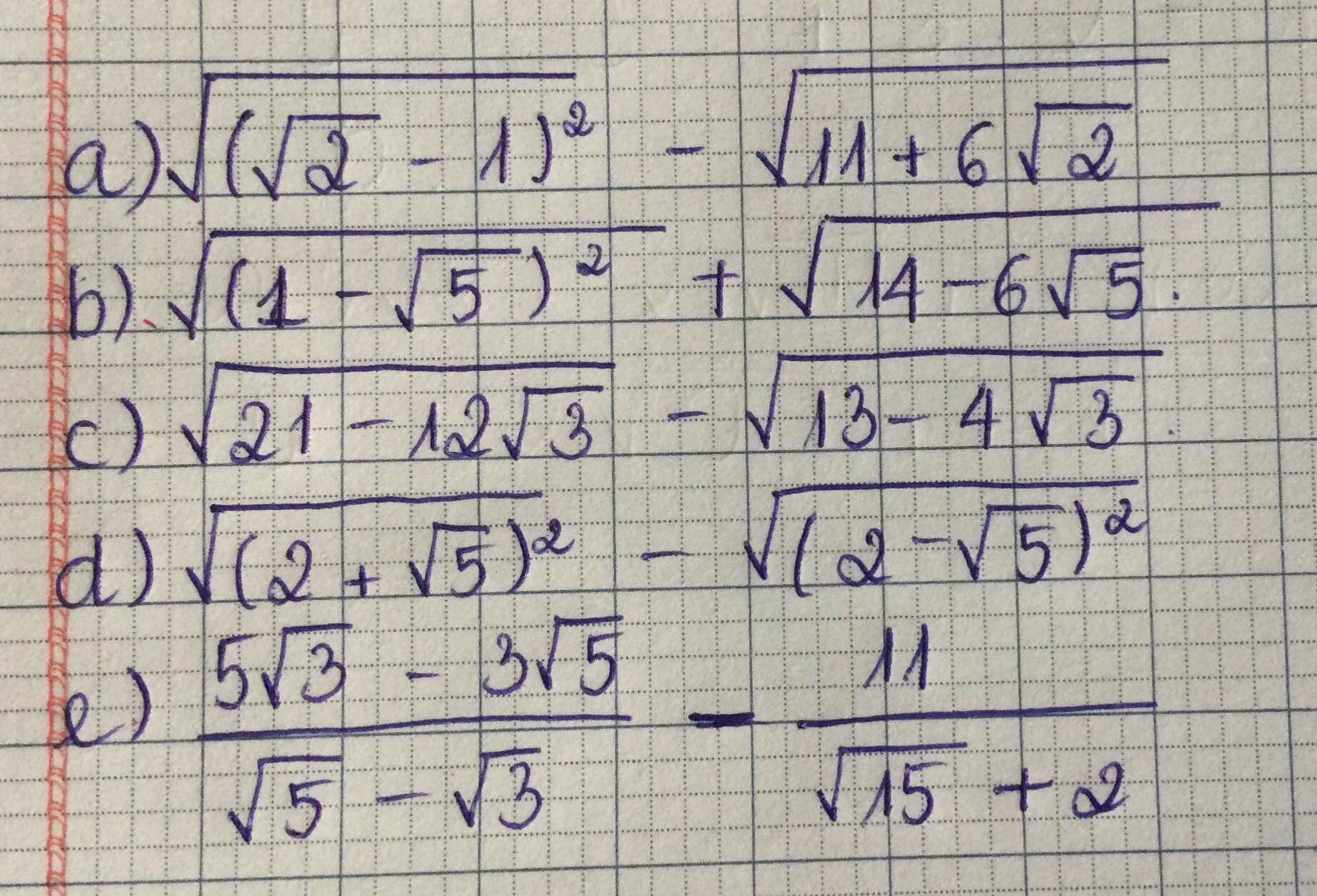 Tính và thu gọn biểu thức.
Tính và thu gọn biểu thức.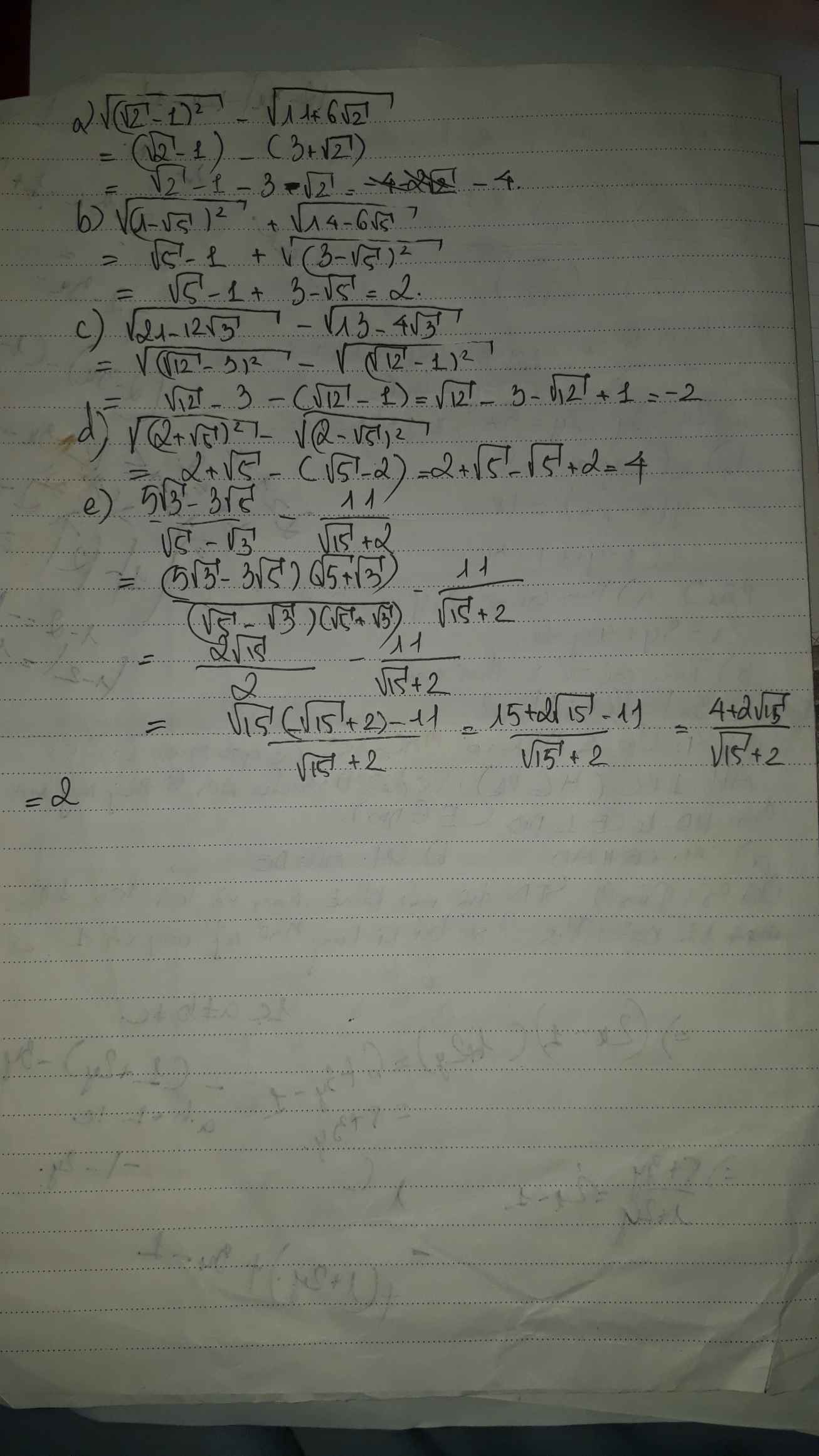
\(\left(2\sqrt{3}+\sqrt{5}\right).\sqrt{3}-\sqrt{60}\)
\(=\)\(2\sqrt{3}.\sqrt{3}+\sqrt{5}.\sqrt{3}-\sqrt{60}\)
\(=\)\(6+\sqrt{15}-\sqrt{60}\)
\(=\)\(6-\sqrt{15}\)
\(\left(2\sqrt{3}+\sqrt{5}\right)\sqrt{3}-\sqrt{60}\)
=\(6+\sqrt{15}-\sqrt{2^2.15}\)
=\(6+\sqrt{15}-2\sqrt{15}\)
=\(6-\sqrt{15}\)
k mk nha