Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(21^{100}-21^{98}< 21^{99}-21^{98}< 21^{99}-21^9\)
\(\Rightarrow21^{100}-21^{98}< 21^{99}-21^9\)

\(a,112882:\left\{22.\left[743-\left(2009-1999\right)\right]\right\}\\ =112882:\left\{22.\left[743-10\right]\right\}\\ =112882:\left(22.733\right)\\ =112882:16126=7\\ b,2200:\left\{320:\left[88-\left(72-16.4\right)\right]\right\}\\ =2200:\left\{320:\left[88-\left(72-64\right)\right]\right\}\\ =2200:\left\{320:\left[88-8\right]\right\}\\ =2200:\left\{320:80\right\}\\ =2200:4=550\\ c,2^4.5-\left\{140-\left[868-12.\left(3087:7^2+4^0\right)\right]\right\}\\ =16.5-\left\{140-\left[868-12.\left(3087:49+1\right)\right]\right\}\\ =80-\left\{140-\left[868-12.\left(63+1\right)\right]\right\}\\ =80-\left\{140-\left[868-12.64\right]\right\}\\ =80-\left\{140-\left[868-768\right]\right\}\\ =80-\left\{140-100\right\}\\ =80-40=40\)
a) 112882 : {22 nhân [743 - (2009 - 1999)]}
Đầu tiên, ta tính trong ngoặc nhọn: 2009 - 1999 = 10
Tiếp theo, ta tính 743 - 10 = 733
Sau đó, ta tính 22 nhân 733 = 16126
Cuối cùng, ta tính 112882 : 16126 = 7
Vậy kết quả của phép tính a) là 7.
b) 2200 : {320 : [88 - (72 - 16 nhân 4)]}
Đầu tiên, ta tính trong ngoặc nhọn: 72 - 16 nhân 4 = 8
Tiếp theo, ta tính 88 - 8 = 80
Sau đó, ta tính 320 : 80 = 4
Cuối cùng, ta tính 2200 : 4 = 550
Vậy kết quả của phép tính b) là 550.
c) 2 mũ 4 nhân 5 - {140 - [868 - 12 nhân (3087 : 7 mũ 2 + 4 mũ 0)]}
Đầu tiên, ta tính trong ngoặc nhọn: 3087 : 7 mũ 2 = 3087 : 49 = 63
Tiếp theo, ta tính 4 mũ 0 = 1
Sau đó, ta tính 12 nhân (63 + 1) = 12 nhân 64 = 768
Tiếp theo, ta tính 868 - 768 = 100
Sau đó, ta tính 140 - 100 = 40
Cuối cùng, ta tính 2 mũ 4 nhân 5 - 40 = 16 nhân 5 - 40 = 80 - 40 = 40
Vậy kết quả của phép tính c) là 40.

1/
Tổng A là tổng các số hạng cách đều nhau 4 đơn vị.
Số số hạng: $(101-1):4+1=26$
$A=(101+1)\times 26:2=1326$
2/
$B=(1+2+2^2)+(2^3+2^4+2^5)+(2^6+2^7+2^8)+(2^9+2^{10}+2^{11})$
$=(1+2+2^2)+2^3(1+2+2^2)+2^6(1+2+2^2)+2^9(1+2+2^2)$
$=(1+2+2^2)(1+2^3+2^6+2^9)$
$=7(1+2^3+2^6+2^9)\vdots 7$

a,= 6-55-55-33+(-9)+(-6).11+22
= 6-(-33)+(-9)+(-66)+22
= 39+(-9)+(-66)+22
= 30+(-44)
= -14
b,= a+(-b)+(-c)+b+(-a)+c+(-c)+b
=[a+(-a)]+[(-b)+b+b]+[-c+c]
= 0+b+0
=b
THE END. :) :3 :D
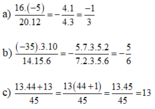
Giải:
a) \(4.2^5:\left(2^3.\dfrac{1}{16}\right)\)
\(=4.2^5:\dfrac{2^3}{16}\)
\(=2^2.2^5:\dfrac{2^3}{2^4}\)
\(=2^7:\dfrac{1}{2}\)
\(=2^6=64\)
Vậy ...
b) \(\dfrac{8^5.10^4.25^3}{16^4.625^3}\)
\(=\dfrac{2^{15}.2^4.5^4.5^6}{2^8.5^{12}}\)
\(=\dfrac{2^{19}.5^{10}}{2^8.5^{12}}\)
\(=\dfrac{2^{11}}{5^2}\)
Vậy ...
c) \(C=2^{200}-2^{199}+2^{198}-2^{197}+...+2^2-2\)
\(\Leftrightarrow C=\left(2^{200}-2^{199}\right)+\left(2^{198}-2^{197}\right)+...+\left(2^2-2\right)\)
\(\Leftrightarrow C=2^{199}\left(2-1\right)+2^{197}\left(2-1\right)+...+2\left(2-1\right)\)
\(\Leftrightarrow C=2^{199}+2^{197}+...+2\)
\(\Leftrightarrow4C=2^{201}+2^{199}+...+2^3\)
\(\Leftrightarrow3C=4C-C=2^{201}-2\)
\(\Leftrightarrow C=\dfrac{2^{201}-2}{3}\)
Vậy ...
Hình như sai rồi