
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(A=\left(\frac{1}{51}+\frac{1}{52}+\frac{1}{53}+...+\frac{1}{75}\right)+\left(\frac{1}{76}+\frac{1}{77}+...+\frac{1}{100}\right)\)
Chia A làm 2 phần,mỗi phân 25 số hạng.
\(A>\frac{25.1}{75}+\frac{25.1}{100}\)
\(A>\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\)
Bé hơn em làm tương tự có điều để nguyên cả 50 p/số.
Chúc em học tốt^^
bạn có thể giải cụ thể hơn cho mình được ko ?
mình chả hiểu gì cả

a) Ta có A = 21 + 22 + 23 + ... + 22022
2A = 22 + 23 + 24 + ... + 22023
2A - A = ( 22 + 23 + 24 + ... + 22023 ) - ( 21 + 22 + 23 + ... + 22022 )
A = 22023 - 2
Lại có B = 5 + 52 + 53 + ... + 52022
5B = 52 + 53 + 54 + ... + 52023
5B - B = ( 52 + 53 + 54 + ... + 52023 ) - ( 5 + 52 + 53 + ... + 52022 )
4B = 52023 - 5
B = \(\dfrac{5^{2023}-5}{4}\)
b) Ta có : A + 2 = 2x
⇒ 22023 - 2 + 2 = 2x
⇒ 22023 = 2x
Vậy x = 2023
Lại có : 4B + 5 = 5x
⇒ 4 . \(\dfrac{5^{2023}-5}{4}\) + 5 = 5x
⇒ 52023 - 5 + 5 = 5x
⇒ 52023 = 5x
Vậy x = 2023
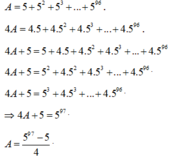
\(A=1+5+5^2+5^3+....+5^{49}+5^{50}\)
\(5A=5+5^2+5^3+5^4+.....+5^{50}+5^{51}\)
\(5A-A=5+5^2+5^3+5^4+......+5^{50}+5^{51}-\left(1+5+5^2+5^3+......+5^{49}+5^{50}\right)\)
\(4A=5+5^2+5^3+5^4+......+5^{50}+5^{51}-1-5-5^2-5^3-5^4-.....-5^{49}-5^{50}\)
\(4A=5^{51}-1\)
\(A=\frac{5^{51}-1}{4}\)