Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=2n^2\left(2n-1\right)-3\left(2n-1\right)+2=\left(2n^2-3\right)\left(2n-1\right)+2\)
Do \(\left(2n^2-3\right)\left(2n-1\right)⋮2n-1\)
\(\Rightarrow2⋮2n-1\)
\(\Rightarrow2n-1=Ư\left(2\right)\)
Mà 2n-1 luôn lẻ \(\Rightarrow2n-1=\left\{-1;1\right\}\)
\(\Rightarrow n=\left\{0;1\right\}\)
2.
\(Q=-\left(x^2+4x+4\right)-\left(y^2-2y+1\right)+7\)
\(Q=-\left(x+2\right)^2-\left(y-1\right)^2+7\le7\)
\(Q_{max}=7\) khi \(\left(x;y\right)=\left(-2;1\right)\)

Ta có : B = \(3x^2+x+5\)
\(=2x^2+x^2+x+\frac{1}{4}+\frac{19}{4}\)
\(=2x^2+\left(x+\frac{1}{2}\right)^2+\frac{19}{4}\)
Vì \(2x^2\ge0\forall x\)
\(\left(x+\frac{1}{2}\right)^2\ge0\forall x\)
Nên : \(B=2x^2+\left(x+\frac{1}{2}\right)^2+\frac{19}{4}\ge0+0+\frac{19}{4}=\frac{19}{4}\)
Vậy \(B_{min}=\frac{19}{4}\) hơ icos vấn đề

Câu b mình viết nhầm dấu \(\ge\)đáng lẽ đúng phải là \(\le\)
a)
\(A=x^2+y^2-x+6y+10.\)
\(=\left(x^2-x+\frac{1}{4}\right)+\left(y^2+6y+9\right)+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Vậy \(MinA=\frac{3}{4}\Leftrightarrow\hept{\begin{cases}\left(x-\frac{1}{2}\right)^2=0\\\left(y+3\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-\frac{1}{2}=0\\y+3=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{1}{2}\\y=-3\end{cases}}}\)
b)
\(B=2x-2x^2-5\)
\(=-2\left(x^2-x+\frac{1}{4}\right)+2.\frac{1}{4}-5\)
\(=-2\left(x-\frac{1}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Vậy \(MaxB=-\frac{9}{2}\Leftrightarrow\left(x-\frac{1}{2}\right)^2=0\Leftrightarrow x-\frac{1}{2}=0\Leftrightarrow x=\frac{1}{2}\)
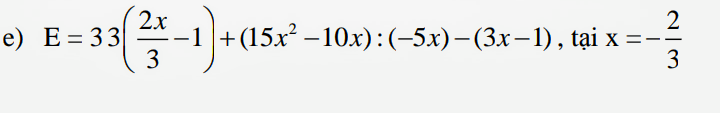
\(E=22x-23-5x+2-3x+1\)
\(=14x-20\)
\(=14\cdot\dfrac{-2}{3}-20=\dfrac{-28}{3}-\dfrac{60}{3}=-\dfrac{88}{3}\)