Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
+ Ban đầu ta có: ảnh thu được trên màn => ảnh thật => d ' = 15 c m , giả sử khi đó vật đang cách thấu kính một đoạn d thì ta có: 1 f = 1 d + 1 15 1
Sau khi dịch vật lại gần thấu kính một đoạn a mà ảnh vẫn thu được trên màn => ảnh dịch ra xa thấu kính => d ' ' = d ' + 5 = 20 c m
⇔ A 2 B 2 A B = 2 A 1 B 1 A B ⇔ 20 d − a = 2.15 d ⇒ d − a = 2 3 d ⇒ 1 f = 3 2 d + 1 20 2
Từ (1) và (2): 1 f = 1 10 ⇒ f = 10 c m

Đáp án: C
HD Giải:
Vì vật dịch lại gần nên ta có d2 = d1 – 3 = 12cm
Ảnh lúc sau cao gấp 2 lần ảnh trước nên
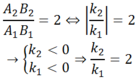


a) Gọi d và d’ là khoảng cách từ điểm sáng S và màn đến thấu kính.




Đáp án: D
HD Giải:
Khi dịch chuyển lại gần thì ảnh dịch ra xa nên phải dịch màn ra xa
d2 = d1 – 10 = 20cm.
Ảnh lúc sau cao gấp 2 lần ảnh trước nên
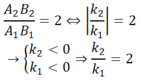
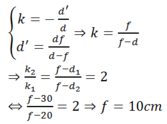

Đáp án: C
Ảnh rõ nét trên màn nên ta có: L = d + d’ = 4m
Ảnh thật nên ngược chiều với vật, do đó k = -3.
Suy ra d’ = 3d → d’ = 3m và d = 1m.
Theo công thức thấu kính:


Đáp án: C
Ảnh rõ nét trên màn nên ta có: L = d + d’
Theo công thức thấu kính:
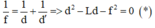
Để có ảnh rõ nét trên màn thì (*) có nghiệm:
∆ ≥ 0 ↔ L ≥ 4 f
Vì chỉ thu được một vị trí cho ảnh rõ nét trên màn nên L = 4f.
Tiêu cự của thấu kính này là: f = L/4 = 1m.




\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};\left\{{}\begin{matrix}d_2=d_1-2\\d_2'=d_1'+b\end{matrix}\right.;\dfrac{A"B"}{A'B'}=\dfrac{5}{3}\Leftrightarrow\dfrac{d_2'.d_1}{d_1'.d_2}=\dfrac{5}{3}\)
\(\Rightarrow\dfrac{\left(d_1'+b\right).d_1}{d_1'.\left(d_1-2\right)}=\dfrac{5}{3}\)\(\Leftrightarrow\dfrac{20\left(d_1'+b\right)}{d_1'\left(20-2\right)}=\dfrac{5}{3}\)
\(\dfrac{A"B"}{A'B'}=\dfrac{5}{3}\Leftrightarrow\dfrac{k_2}{k_1}=\dfrac{f-d_1}{f-d_2}=\dfrac{5}{3}\Leftrightarrow\dfrac{f-20}{f-20+2}=\dfrac{5}{3}\Rightarrow f=....\)
\(\Rightarrow d_1'=\dfrac{fd_1}{d_1-f}=...;\dfrac{20\left(d_1'+b\right)}{18d_1'}=\dfrac{5}{3}\Rightarrow b=...\)
30cm