(Vật lí 9) Câu hỏi: Hãy dựng ảnh của thấu kính hội tụ về vật nằm ngoài tiêu điểm d=2f và f <d <2f

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

TH

Tinh Hiên

10 tháng 5 2020

(Vật lí 9)

Câu hỏi: Hãy dựng ảnh của thấu kính hội tụ về vật nằm ngoài tiêu điểm d=2f và f <d <2f

#Vật lý lớp 9

1

Y

❤ ~~ Yến ~~ ❤

10 tháng 5 2020

Hỏi đáp Vật lý

Các câu hỏi dưới đây có thể giống với câu hỏi trên

P

phantuananh

13 tháng 2 2016

1 vật sáng AB hình dạng mũi tên đặt vuông góc với trục chính của thấu kính hội tụ cách thấu kính hội tụ 1 khoảng bằng d . vẽ trong trường hợp sau :a, d<F ( F là tiêu điểm )b, F<d<2Fc,d=Fd, d>2Fe, d<2FRỒI so sánh ảnh của vật qua hình xẽ . chứng minh điều so sánh bằng công thức toán học sắp đi học rùi ai giải giúp mk với giải giúp mk thep cách lớp 9...

#Vật lý lớp 9

2

HD

Hà Đức Thọ

Admin

13 tháng 2 2016

a) Vẽ hình

O A B B' A' F K

Từ hình vẽ ta thấy: Ảnh là ảnh ảo, lớn hơn vật.

Chứng minh bằng hình học:

Gọi f là tiêu cự, là khoảng cách từ tiêu điểm F đến O.

d là khoảng cách từ vật đến O

d' là khoảng cách từ ảnh đến O

Ta có:

- Tam giác AOB đồng dạng với A'OB' \(\Rightarrow \dfrac{OB}{OB'}=\dfrac{AB}{A'B'}\)(1)

- Tam giác KFO đồng dạng với A'FB' \(\Rightarrow \dfrac{OF}{B'F'}=\dfrac{OK}{A'B'}\)

Mà \(OK=AB\)

\(\Rightarrow \dfrac{OF}{B'F'}=\dfrac{OB}{OB'}\Rightarrow \dfrac{f}{d'+f}=\dfrac{d}{d'}\Rightarrow d'f=dd'+df\Rightarrow d'(f-d)=df\Rightarrow d'=\dfrac{df}{f-d}\) (2)

Từ (1) ta có: \(\dfrac{A'B'}{AB}=\dfrac{d'}{d}\)

Thế d' ở (2) vào ta có: \(\dfrac{A'B'}{AB}=\dfrac{f}{f-d}\)

Vì \(d< f\) nên \(\dfrac{f}{f-d} > 1 \Rightarrow \dfrac{A'B'}{AB}> 1\)

Do đó, ảnh lớn hơn vật.

Các câu khác, bạn vẽ hình và chứng minh tương tự nhé.

HD

Hà Đức Thọ

Admin

13 tháng 2 2016

Bạn vẽ hình ra, rồi dùng mấy định lý tam giác đồng dạng để chứng minh.

MB

Menna Brian

7 tháng 3 2022

Đặc điểm của thấu kính hội tụ ? Ba tia sáng đặc biệt của thấu kính hội tụ ? Đặc điểm của ảnh của một vật tạo bởi thấu kính hội tụ ? Vẽ ảnh của vật AB tạo bởi TKHT ; nêu đặc điểm ảnh trong các trường hợp : d > 2f ; d = 2f ; f < d < 2f ; d < f

#Vật lý lớp 9

0

TC

Thanh Chiêm

23 tháng 3 2023

Vật sáng AB có độ cao h= 2 cm, được đặt vuông góc trước một thấu kính hội tụ có tiêu cự d. Điểm A cách thấu kính một khoảng d=2f. Cho biết tiêu cự của thấu kính f=2cm A. Dựng ảnh A'B'của AB tạo bởi thấu kính hội tụ B. Tính chiều cao h'của ảnh và khoảng cách d'từ ảnh tới quang tâm.

#Vật lý lớp 9

0

XH

Xuân Huy

9 tháng 5 2023

1.Vật sáng AB có độ cao h=5cm được đặt vuông góc trước một thấu kính hội tụ có tiêu cự f=10cm, điểm A cách thấu kính một khoảng d = 2f. Hãy dựng ảnh A B của AB rồi tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh.2.Vật sáng AB được đặt vuông góc với trục chính của thấu kính phân kì có tiêu cự f= 18cm. Điểm A năm trên trục chính và cách thấu kính một khoảng d = 36cm, AB...

#Vật lý lớp 9

0

HD

Hoàng Đức Long

26 tháng 1 2019

Vật AB có độ cao h được đặt vuông góc trước một thấu kính hội tụ tiêu cự f như hình 42-43.5 SBT. Điểm A nằm trên trục chính cách thấu kính một khoảng d = 2f. Dựng ảnh A'B' của AB tạo bởi thấu kính đã...

#Vật lý lớp 9

1

VT

Vũ Thành Nam

26 tháng 1 2019

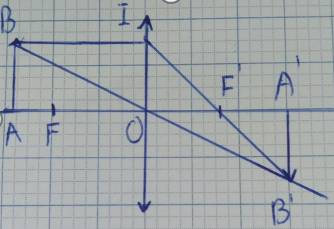
Dựng ảnh của vật sáng AB qua thấu kính hội tụ. Dùng hai trong ba tia sáng đã học để dựng ảnh B’ của điểm B.

+ Vật AB cách thấu kính d = 2f, vật ngoài khoảng OF.

Tia BI đi song song với trục chính nên cho tia ló đi qua F’

Tia tới BO là tia đi quang tâm O nên cho tia ló đi thẳng

Hai tia ló trên giao nhau tại B’, ta thu được ảnh thật B’ của B qua thấu kính.

Từ B’ hạ vuông góc với trục của thấu kính, cắt trục chính tại điểm A’. A’ là ảnh của điểm A. A’B’ là ảnh của AB tạo bởi thấu kính hội tụ.

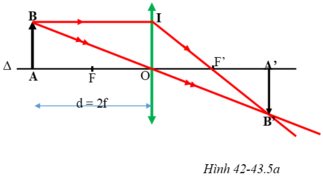
Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

HD

Hoàng Đức Long

3 tháng 6 2019

Vật sáng AB có độ cao h được đặt vuông góc trước một thấu kính hội tụ có tiêu cự f, điểm A cách thấu kính một khoảng d = 2f (hình vẽ)a) Dựng ảnh A’B’ của AB tạo bởi thấu kính hội tụ.b) Vận dụng kiến thức hình học tinh chiều cao h’ cảu ảnh và khoảng cách từ ảnh tới quang...

#Vật lý lớp 9

1

VT

Vũ Thành Nam

3 tháng 6 2019

a) Sử dụng hai trong ba tia đặc biệt để vẽ ảnh.

b) Dựa vào tam giác đồng dạng, suy ra h’ = h; d’ = d = 2f.

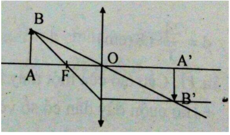
Đề kiểm tra Vật Lí 9

HD

Hoàng Đức Long

4 tháng 2 2017

Đặt một vật AB hình mũi tên vuông góc với trục chính của thấu kính hội tụ tiêu cự f và cách thấu kính một khoảng d > 2f thì ảnh A’B’ của AB qua thấu kính là: A. ảnh thật, ngược chiều và nhỏ hơn vật B. ảnh thật, cùng chiều và nhỏ hơn vật C. ảnh thật, ngược chiều và lớn hơn vật D. ảnh thật, cùng chiều và lớn hơn vật....

#Vật lý lớp 9

1

VT

Vũ Thành Nam

4 tháng 2 2017

=> Khi đặt vật AB vuông góc với trục chính của thấu kính hội và cách thấu kính một khoảng d > 2f thì ảnh A’B’ của AB qua thấu kính là ảnh thật ngược chiều với vật và nhỏ hơn vật

Đáp án: A

HD

Hoàng Đức Long

13 tháng 2 2019

Vật AB có độ cao h được đặt vuông góc trước một thấu kính hội tụ tiêu cự f như hình 42-43.5 SBT. Điểm A nằm trên trục chính cách thấu kính một khoảng d = 2f. Vận dụng kiến thức hình học, tính chiều cao h' của ảnh theo h và tính khoảng cách từ d' từ ảnh đến thấu kính theo...

#Vật lý lớp 9

1

VT

Vũ Thành Nam

13 tháng 2 2019

Trên hình 42-43.5a, xét hai cặp tam giác đồng dạng:

ΔABO và ΔA’B’O; ΔA’B’F’ và ΔOIF’.

Từ hệ thức đồng dạng được: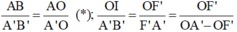 Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

Vì AB = OI (tứ giác BIOA là hình chữ nhật)

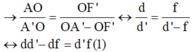
Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

Chia cả hai vế của (1) cho tích d.d’.f ta được:

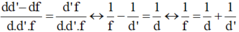
Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

(đây được gọi là công thức thấu kính cho trường hợp ảnh thật)

Thay d = 2f, ta tính được: OA’ = d’ = 2f = d

Thay vào (*) ta được: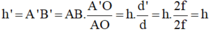 Giải SBT Vật Lí 9 | Giải bài tập Sách bài tập Vật Lí 9

Vậy d’ = d; h’ = h.

XV

xin vĩnh biệt lớp 9

19 tháng 4 2023

Câu 8: Vật sáng AB hình mũi tên chiều từ A đến B được đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự f = 10cm. Điểm A nằm trên trục chính. Vật AB cách thấu kính một khoảng d = 30cm.a. Hãy dựng ảnh A’B’ của AB và nhận xét về đặc điểm của ảnh này?b.Tính khoảng cách từ ảnh đến thấu kính và chiều cao của ảnh. Cho biết vật AB có chiều cao h =...

#Vật lý lớp 9

1

H9

HT.Phong (9A5)

CTVHS

19 tháng 4 2023

Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Leftrightarrow\dfrac{d}{h}=\dfrac{d'}{h'}\Leftrightarrow\dfrac{d'}{h'}=\dfrac{30}{5}\Leftrightarrow d'=6h'\)

Áp dụng công thức tính thấu kính ta có:

\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{30}+\dfrac{1}{6h'}\)

\(\Rightarrow h'=2,5\left(cm\right)\)

Vậy ảnh có chiều cao của ảnh là

Khoảng cách từ ảnh đến thấu kính:

Ta có: \(d'=6h'=6.2,5=15\left(cm\right)\)

XV

xin vĩnh biệt lớp 9

19 tháng 4 2023

d , d' , h , h' là gì thế bạn ?