Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

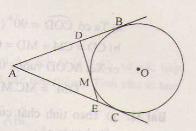
Chứng minh AB=AC; DB=DM và EC=EM.
Chu vi ΔADE bằng
= AD + DM + ME + AE
= AD + DB + EC + AE
= AB + AC
= 2AB.
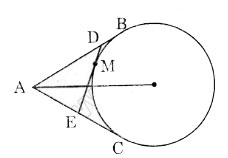
Ta có AB = AC; DB = DM;
EC = EM.
Chu vi Δ ADE:
AD +AE +DE = AD +DM + AE + EM
=AD + DB + AE + EC = AB + AC = 2AB

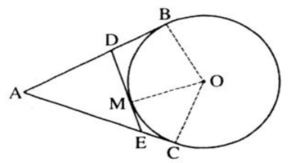
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

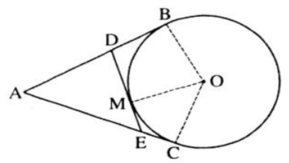
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

Ta có
DB=DM; EC=EM; AB=AC (2 tiếp tuyến cùng xp từ 1 điểm ngoài đường tròn thì khoảng cách từ điểm đó đến các tiếp điểm = nhau)
\(C_{ADE}=AD+DM+AE+EM=AD+DB+AE+EC=\)
\(=AB+AC=2AB\)

Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC, AB = AC
Chu vi ΔADE:
CΔADE = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB (đpcm)

Đáp án B
* Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB = AC; DB = DM; EM = EC
suy ra: DE = DM + ME = DB + EC.
* Chu vi tam giác ADE là:
AD + AE + DE = AD + AE + DB + EC
= (AD + DB ) + ( AE + EC ) = AB + AC = 2AB ( vì AB = AC )
A D B O E C M
Theo tính chất hai tiếp tuyến cắt nhau ta có:
DM = DB, EM = EC , AB = AC
Chu vi \(\Delta ADE\):
\(C_{\Delta ADE}\) = AD + DE + AE = AD + DM + ME + AE = AD + DB + EC + AE = AB + AC = 2AB ( đpcm )