Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có AH.AO=AB^2 ( theo hệ thức lượng)
AM.AN=BC^2 (bạn xét tam giác ACM và ANC đồng dạng theo trường hợp g-g)
Mà AB=AC (t/c 2 tt cắt nhau) ===> AH.AO=AM.AN

a: Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
nên ABOC là tứ giác nội tiếp
Tâm là trug điểm của AO
b: Xét (O) có
AB là tiếp tuýen
AC là tiếp tuyến
Do đó: AB=AC
mà OB=OC
nên OA là đường trung trực của BC
Xét ΔOBA vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(1\right)\)
Xét ΔABM và ΔANB có
\(\widehat{ABM}=\widehat{ANB}\)
\(\widehat{BAM}\) chung
Do đo; ΔABM\(\sim\)ΔANB
Suy ra: AB/AN=AM/AB
hay \(AB^2=AN\cdot AM\left(2\right)\)
Từ (1) và (2) suy ra \(AH\cdot AO=AM\cdot AN\)


a) Vì AB,AC là tiếp tuyến của (O) \(\Rightarrow\hept{\begin{cases}AB\perp OB\\AC\perp OC\end{cases}\Rightarrow}\hept{\begin{cases}\widehat{ABO}=90^0\\\widehat{ACO}=90^0\end{cases}}\)
Xét tứ giác ABOC có \(\widehat{ABO}+\widehat{ACO}=180^0\)
Mà 2 góc này ở vị trí đối nhau trong tứ giác ABOC
\(\Rightarrow ABOC\)nội tiếp ( dhnb )
b) Xét (O) có AB là tiếp tuyến tại B ; MB là dây cung
\(\Rightarrow\widehat{ABM}=\widehat{ANB}\left(=\frac{1}{2}sđ\widebat{MB}\right)\)
Xét tam giác ABM và tam giác ANB có:
\(\hept{\begin{cases}\widehat{BAN}chung\\\widehat{ABM}=\widehat{ANB}\left(cmt\right)\end{cases}\Rightarrow\Delta ABM~\Delta ANB\left(g-g\right)}\)
\(\Rightarrow\frac{AB}{AM}=\frac{AN}{AB}\Rightarrow AB^2=AM.AN\left(1\right)\)
c) Gọi H là giao điểm của BC và AO
Xét tam giác ABH và tam giác AOB có:
\(\hept{\begin{cases}\widehat{BAO}chung\\\widehat{AHB}=\widehat{ABO}=90^0\end{cases}}\Rightarrow\Delta ABH~\Delta AOB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AH}=\frac{AO}{AB}\Rightarrow AB^2=AO.AH\left(2\right)\)
Từ (1) và (2) \(\Rightarrow AM.AN=AH.AO\)
\(\Rightarrow\frac{AM}{AH}=\frac{AO}{AN}\)
Xét tam giác AMH và tam giác AON có:
\(\hept{\begin{cases}\widehat{NAO}chung\\\frac{AM}{AH}=\frac{AO}{AN}\left(cmt\right)\end{cases}\Rightarrow\Delta AMH~\Delta AON\left(c-g-c\right)}\)
\(\Rightarrow\widehat{AHM}=\widehat{ANO}\)
Mà \(\widehat{AHM}+\widehat{MHO}=180^0\)
\(\Rightarrow\widehat{ANO}+\widehat{MHO}=180^0\)
Xét tứ giác MHON có
\(\widehat{ANO}+\widehat{MHO}=180^0\)mà 2 góc này ở vị trí đối nhau trong tứ giác MHON
\(\Rightarrow MHON\)nội tiếp ( dhnb )
\(\Rightarrow\widehat{NMO}=\widehat{NHO}\left(3\right)\)
Vì H là giao điểm của BC và AO ( h.vẽ )
Mà \(AB,AC\)là tiếp tuyến của (O)
\(\Rightarrow BC\perp OA\)
\(\Rightarrow\widehat{BHO}=90^0\)
Vì NF là tiếp tuyến của (O) tại N
\(\Rightarrow\widehat{ÒNF}=90^0\)
Xét tứ giác FHON có:\(\widehat{FHO}+\widehat{FNO}=180^0\)mà 2 góc này ở vị trí đối nhau trong tứ giác FHON
=> FHON nội tiếp ( dhnb )
\(\Rightarrow\widehat{NHO}=\widehat{NFO}\left(4\right)\)
Từ (3) và (4) \(\Rightarrow\widehat{NMO}=\widehat{NFO}\)
\(\Rightarrow FMON\)nội tiếp (dhnb)
\(\Rightarrow\widehat{FMO}+\widehat{FNO}=180^0\)
\(\Rightarrow\widehat{FMO}=90^0\)
\(\Rightarrow FM\perp OM\)
\(\Rightarrow FM\)là tiếp tuyến của (O)
d) Vì E thuộc đường tròn ngoại tiếp tam giác MNO
\(\Rightarrow E\)thuộc đường tròn đường kính OF
\(\Rightarrow\widehat{OEF}=90^0\)
+) Vì E thuộc đường tròn ngoại tiếp tứ giác ABOC hay E thuộc đường tròn đường kính AO
\(\Rightarrow\widehat{AEO}=90^0\)
\(\Rightarrow\widehat{OEF}+\widehat{AEO}=180^0\)
\(\Rightarrow A,E,F\)thẳng hàng
Lại có vì góc AEO= 90 độ \(\Rightarrow OE\perp AF\left(5\right)\)
Gọi K là trung điểm của MN
\(\Rightarrow OF\perp MN\)
\(\Rightarrow AK\perp OF\)
Xét tam giác AOF có: \(\hept{\begin{cases}AK\perp OF\\FH\perp AO\end{cases}}\)mà AK cắt FH tại P
=> P là trực tâm của tam giác AOF
\(\Rightarrow OP\perp AF\left(6\right)\)
Từ (5) và (6) \(\Rightarrow O,E,P\)thẳng hàng ( đpcm )

Vì \(\widehat{ABO}\)là góc tạo bởi tia tiếp tuyến AB và dây cung BD ( đường kính AB )
\(\Rightarrow\widehat{ABO}=\frac{1}{2}.\widehat{BOD}=\frac{1}{2}.180^o=90^o\)
Chứng mình ương tự với \(\widehat{ACO}\), suy ra \(\widehat{ACO}=90^o\)
Xét tứ giác ABOC có :
Góc ABO và góc ACO là hai góc đối
\(\widehat{ABO}+\widehat{ACO}=90^o+90^o=180^o\)
=> Tứ giác ABOC nội tiếp đường tròn ( theo tính chất tổng hai góc đối bằng 180 độ ... )
Gọi I là trung điểm của AB
Có tam giác ABO vuông tại B, trung tuyến là BI
=> BI = 1/2.AO=AI=IO (1)
Tam giác ACO vuông tại C, có trung tuyến là CI
=> CI=1/2.AO=AI=IO (2)
Từ (1) và (2) => BI = AI = IO = IC
=> I cách đều 4 đỉnh tứ giác ABOC
=> I là tâm đường tròn ngoại tiếp tứ giác ABOC , có bán kinh R= 1/2.AO


a) Hai tam giác vuông ABO và ACO có chung cạnh huyền AO nên A, B, O, C cùng thuộc đường tròn đường kính AO.
Vậy tứ giác ABOC là tứ giác nội tiếp.
b) Ta thấy ngay \(\Delta ABD\sim\Delta AEB\left(g-g\right)\)
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AE.AD=AB^2\)
Xét tam giác vuông ABO có BH là đường cao nên áp dụng hệ thức lượng ta có:
\(AH.AO=AB^2\)
Suy ra AD.AE = AH.AO
c) Ta có \(\widehat{PIK}+\widehat{IKQ}+\widehat{P}+\widehat{Q}=360^o\)
\(\Rightarrow2\left(\widehat{PIO}+\widehat{P}+\widehat{OKQ}\right)=360^o\)
\(\Rightarrow\widehat{PIO}+\widehat{P}+\widehat{OKQ}=180^o\)
Mặt khác \(\widehat{PIO}+\widehat{P}+\widehat{IOP}=180^o\)
\(\Rightarrow\widehat{IOP}=\widehat{OKQ}\Rightarrow\Delta PIO\sim\Delta QOK\)
\(\Rightarrow\frac{IP}{PO}=\frac{OQ}{KQ}\Rightarrow PI.KQ=PO^2\)
Sử dụng bất đẳng thức Cô-si ta có:
\(IP+KQ\ge2\sqrt{IP.KQ}=2\sqrt{OP^2}=PQ\)
acje cho hỏi 2 tam giác đồng dạng ở câu b là góc nào í chỉ ro rõ cho e với ạk

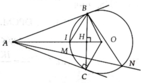
a, A B M ^ = A N B ^ = 1 2 s đ B M ⏜
Chứng minh được: ∆ABM:∆ANB (g.g) => ĐPCM
b, Chứng minh AO ^ BC áp dụng hệ thức lượng trong tam giác vuông ABO và sử dụng kết quả câu a) Þ AB2 = AH.AO
c, Chứng minh được A B I ^ = C B I ^ B I ⏜ = C I ⏜ => BI là phân giác A B C ^ . Mà AO là tia phân giác B A C ^ => I là tâm đường tròn nội tiếp ∆ABC
