Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Nam ủng hộ x tờ tiền mệnh giá 20 nghìn đồng, tương ứng 20.x nghìn đồng
Và y tờ tiền mệnh giá 50 nghìn đồng, tương ứng 50.y nghìn đồng
Tổng số tiền ủng hộ là: \(20x + 50y\) (nghìn đồng)
b) Vì số tiền ủng hộ (\(20x + 50y\)nghìn đồng) phải nhỏ hơn hoặc bằng có tiền Nam có (700 nghìn đồng) nên ta có bất đẳng thức: \(20x + 50y \le 700\)

Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ vẽ không quá 30 giờ nên \(2x + 3y \le 30\)
- Số tấm thiệp tối thiểu là 12 tấm nên \(x + y \ge 12\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
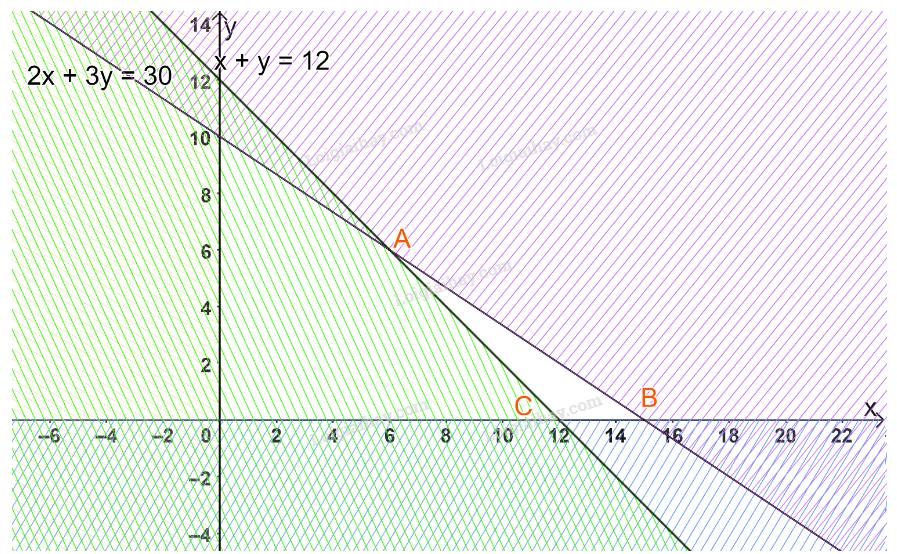
Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(A(6;6),\)\(B(15;0),\)\(C(12;0).\)
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: \(F = 10x + 20y\)
Tính giá trị của F tại các đỉnh của tam giác:
Tại \(A(6;6):\)\(F = 10.6 + 20.6 = 180\)
Tại \(B(15;0):\)\(F = 10.15 + 20.0 = 150\)
Tại \(C(12;0):\)\(F = 10.12 + 20.0 = 120\)
F đạt giá trị lớn nhất bằng 180 tại \(A(6;6).\)
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.

Tham khảo
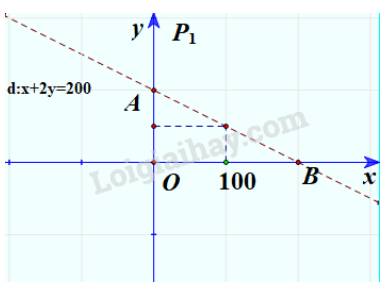
Bước 1:
Gọi x là số phút gọi nội mạng (\(x \in \mathbb{N}\)), y là số phút gọi ngoại mạng (\(y \in \mathbb{N}\))
Số tiền cần phải trả là \(x + 2y\) nghìn đồng.
Để số tiền phải trả ít hơn 200 nghìn đồng thì \(x + 2y < 200\).
Như vậy, bài toán trở thành tìm miền nghiệm của bất phương trình \(x + 2y < 200\)
Bước 2:
Xác định miền nghiệm:
+ Vẽ đường thẳng d: x+2y=200 (nét đứt).
+ Thay tọa độ O(0;0) vào biểu thức x+2y ta được 0+2.0=0<200
=> Miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d.
Vậy nếu số phút sử dụng nội mạng là x và ngoại mạng là y mà điểm (x;y) nằm trong miền tam giác OAB không kể đoạn AB thì số tiền phải trả thấp hơn 200 nghìn đồng.
Chú ý
x và y là số tự nhiên nên cần lấy phần không âm của trục Ox và phần không âm của trục Oy.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
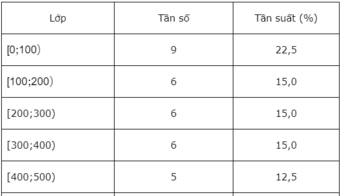
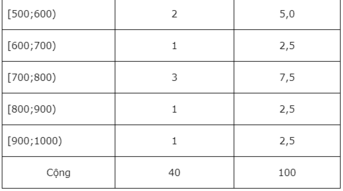
b) b) Cộng các tần suất của bốn lớp [300;400), [400;500), [500;600), [600;700) ta được 15+ 12,5+ 5+ 2,5 = 35. Đáp án là B.

Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.

Từ dãy số liệu ta có bảng phân bố tần số - tần suất ghép lớp sau đây:
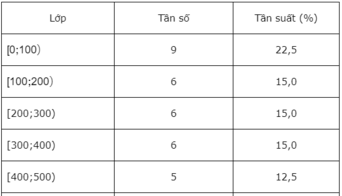
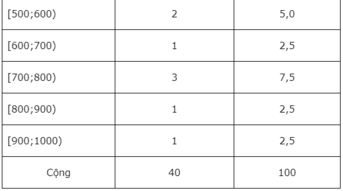
c) Cộng các tần suất của năm lớp [500;600), [600;700), [700;800), [800;900) và [900;1000) ta được . Đáp án là B.

a)
Nếu \(0 < x \le 2\) thì \(T(x) = 1,2x\) (triệu đồng)
Nếu \(x > 2\) thì \(T(x) = 1,2.2 + 0,9.(x - 2) = 0,9x + 0,6\) (triệu đồng)
Số tiền phải trả sau khi thuê x ngày là
\(T(x) = \left\{ \begin{array}{l}1,2x\quad \quad \quad \;(0 < x \le 2)\\0,9x + 0,6\quad (x > 2)\end{array} \right.\)
b) \(T(2) = 1,2.2=2,4\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 2 ngày là 2,4 triệu đồng
\(T(3) = 0,9.3+0,6 = 3,3\) (triệu đồng)
Ý nghĩa: số tiền khách phải trả khi thuê 3 ngày là 3,3 triệu đồng
\(T(5) = 0,9.5+0,6=5,1\)
Ý nghĩa: số tiền khách phải trả khi thuê 5 ngày là 5,1 triệu đồng


Trường hợp 1: \(x = 2,y = 3\)
\( \Rightarrow \)Số tiền Nam ủng hộ là: \(2.20 + 3.50 = 190\) (nghìn đồng) \( < 700\) nghìn đồng (thỏa mãn).
Trường hợp 2: \(x = 15,y = 10\)
\( \Rightarrow \)Số tiền Nam ủng hộ là: \(15.20 + 10.50 = 800\) (nghìn đồng) \( > 700\) nghìn đồng (không thỏa mãn).