Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M(x,y)
Trong (E) có : \(c=\sqrt{a^2-b^2}=\sqrt{5}\)
Từ đó ta có : \(F_1\left(\sqrt{5};0\right);F_2\left(-\sqrt{5};0\right)\); \(F_1F_2=2\sqrt{5}\)
=> \(\overrightarrow{F_1M}\left(x-\sqrt{5};y\right)\Rightarrow F_1M^2=\left(x-\sqrt{5}\right)^2+y^2\)
tương tự \(F_2M^2=\left(x+\sqrt{5}\right)^2+y^2\)
Do \(\widehat{F_1MF_2}=90^{\text{o}}\) nên tam giác F1MF2 vuông tại M
=> F1M2 + F2M2 = F1F22
<=> \(\left(x-\sqrt{5}\right)^2+y^2+\left(x+\sqrt{5}\right)^2+y^2=20\)
\(\Leftrightarrow x^2+y^2=5\)
Lại có \(M\in\left(E\right)\Rightarrow\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\)
từ đó ta có hệ \(\left\{{}\begin{matrix}x^2+y^2=5\\\dfrac{x^2}{9}+\dfrac{y^2}{4}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2=\dfrac{9}{5}\\y^2=\dfrac{16}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\pm\dfrac{3\sqrt{5}}{5}\\y=\pm\dfrac{4\sqrt{5}}{5}\end{matrix}\right.\)

Đồ thị của hàm số (*) vừa tìm được có dạng là hàm số bậc 2 khuyết b và c tập hợp các điểm cách đều nhau qua một đường thẳng, đồ thị của hàm bậc 2 này có tên gọi là parabol.

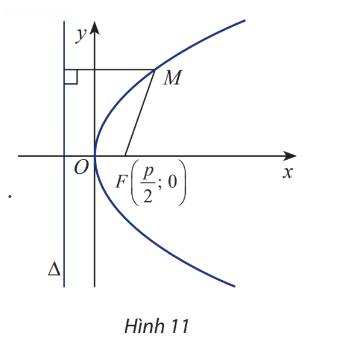
a) Ta có: \(\overrightarrow {FM} = \left( {x - \frac{p}{2};y} \right) \Rightarrow MF = \left| {\overrightarrow {FM} } \right| = \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} \)
\(d\left( {M,\Delta } \right) = \frac{{\left| {x + \frac{p}{2}} \right|}}{1} = \left| {x + \frac{p}{2}} \right|\)
b) M thuộc parabol (P) nên M cách đều F và \(\Delta \)
Suy ra \(MF = d\left( {M,\Delta } \right) \Leftrightarrow \sqrt {{{\left( {x - \frac{p}{2}} \right)}^2} + {y^2}} = \left| {x - \frac{p}{2}} \right|\)

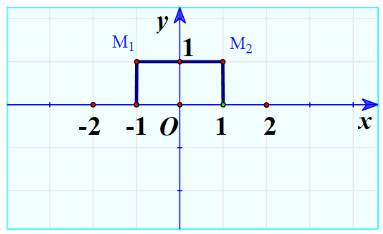
a) Thay \({x_1} = - 1;{x_2} = 1\) vào \(y = {x^2}\) ta được:
\({y_1} = f\left( { - 1} \right) = {\left( { - 1} \right)^2} = 1\)
\({y_2} = f\left( 1 \right) = {1^2} = 1\)
b) Ta có \({x_1} = - 1;{y_1} = 1 \Rightarrow {M_1}\left( { - 1;1} \right)\)
Ta có: \({x_2} = 1;{y_2} = 1 \Rightarrow {M_2}\left( {1;1} \right)\)
Biểu diễn trên mặt phẳng:

\(a=2;b=1\Rightarrow c=\sqrt{3}\)
\(\Rightarrow F_1F_2=2c=2\sqrt{3}\)
\(MF_1\perp MF_2\Rightarrow\Delta MF_1F_2\) vuông tại M
\(\Rightarrow MF_1^2+MF_2^2=F_1F_2^2=12\) (Pitago)
Ta có: \(\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1+MF_2=2a=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\\left(MF_1+MF_2\right)^2=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1^2+MF_2^2+2MF_1MF_2=16\end{matrix}\right.\)
\(\Rightarrow MF_1.MF_2=2\)
\(\Rightarrow S_{MF_1F_2}=\frac{1}{2}MF_1.MF_2=1\)

a)
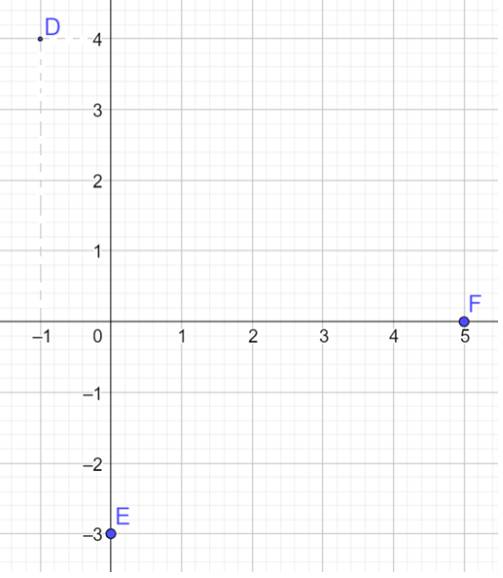
b) Vì tọa độ vectơ \(\overrightarrow {OM} \) chính là tọa độ của điểm M (với mọi M) nên ta có:
\(\overrightarrow {OD} = \left( { - 1;4} \right),\overrightarrow {OE} = \left( {0; - 3} \right),\overrightarrow {OF} = \left( {5;0} \right)\)
c)
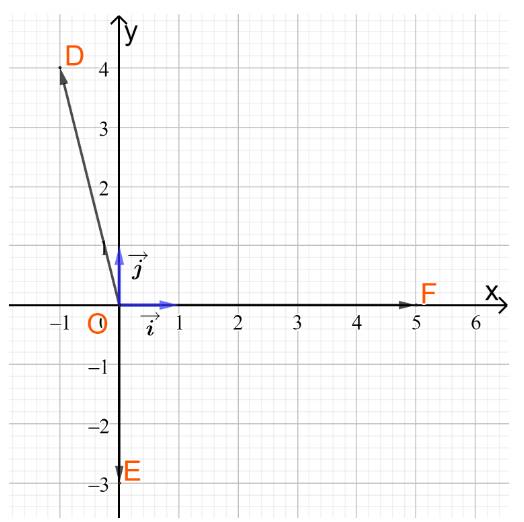
Từ hình vẽ ta có tọa độ của hai vectơ và \(\overrightarrow j \)là
và \(\overrightarrow j = (0;1)\)

\(1.x^2+\dfrac{1}{x^2}-2m\left(x+\dfrac{1}{x}\right)+1+2m=0\left(1\right)\)\(đặt:x^2+\dfrac{1}{x^2}=t\)
\(x>0\Rightarrow t\ge2\sqrt{x^2.\dfrac{1}{x^2}}=2\)
\(x< 0\Rightarrow-t=-x^2+\dfrac{1}{\left(-x^2\right)}\ge2\Rightarrow t\le-2\)
\(\Rightarrow t\in(-\infty;-2]\cup[2;+\infty)\left(2\right)\)
\(\Rightarrow\left(1\right)\Leftrightarrow t^2-2mt+2m-1=0\)
\(\Leftrightarrow\left(t-1\right)\left(t-2m+1\right)=0\Leftrightarrow\left[{}\begin{matrix}t=1\notin\left(2\right)\\t=2m-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}2m-1\le-2\\2m-1\ge2\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{3}{4}\end{matrix}\right.\)
\(2.\) \(f^2\left(\left|x\right|\right)+\left(m-2\right)f\left(\left|x\right|\right)+m-3=0\left(1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=3-m\end{matrix}\right.\)
\(dựa\) \(vào\) \(đồ\) \(thị\) \(f\left(\left|x\right|\right)\) \(\Rightarrow f\left(\left|x\right|\right)=-1\) \(có\) \(2nghiem\) \(pb\)
\(\left(1\right)có\) \(6\) \(ngo\) \(pb\Leftrightarrow\left\{{}\begin{matrix}-1< 3-m< 3\\3-m\ne-1\\\end{matrix}\right.\)\(\Leftrightarrow0< m< 4\)
\(\Rightarrow m=\left\{1;2;3\right\}\)