Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
+Phương trình chính tắc của elip có dạng:
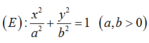
Nên a= 4; b= 2
+Vì MF1= MF2 nên M thuộc đường trung trực của F1F2 chính là trục Oy
+ M là điểm thuộc (E) nên M là giao điểm của elip và trục Oy
Vậy . M1(0 ; 2) và M2(0; -2).

(E) \(\frac{x^2}{16}+\frac{y^2}{4}=1\)
MF1 = MF2 => M thuộc đường trung trực của F1 F2 => M thuộc Oy
=> M( 0; m )
Vì M thuộc E nên ta có: \(\frac{m^2}{4}=1\)=> m = 2 hoặc m = - 2
=> M(0; 2) hoặc M ( 0 ; -2)

Đáp án B
- Giả sử:
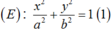
Theo giả thiết thì : c = 4 nên a2- b2= 16 (2)
(E) qua A suy ra :
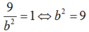
thay vào (2) ta có:
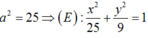
M thuộc (E)
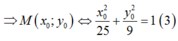
Theo tính chất của (E) ta có bán kính qua tiêu
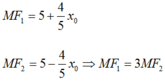
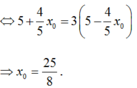
Thay vào ta có:
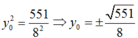

Đáp án D
Phương trình chính tắc của elip có dạng:
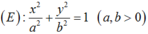
Theo giải thiết ta có c = 4
Chu vi của tam giác MF1F2 bằng 18 nên
MF1+ MF2+ F1F2 = 2a+ 2c nên 2a+ 2c= 18
Mà c= 4 => a= 5




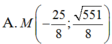
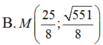
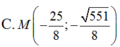
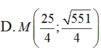
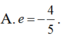
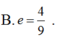
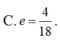
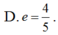
\(a=2;b=1\Rightarrow c=\sqrt{3}\)
\(\Rightarrow F_1F_2=2c=2\sqrt{3}\)
\(MF_1\perp MF_2\Rightarrow\Delta MF_1F_2\) vuông tại M
\(\Rightarrow MF_1^2+MF_2^2=F_1F_2^2=12\) (Pitago)
Ta có: \(\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1+MF_2=2a=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\\left(MF_1+MF_2\right)^2=16\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}MF_1^2+MF_2^2=12\\MF_1^2+MF_2^2+2MF_1MF_2=16\end{matrix}\right.\)
\(\Rightarrow MF_1.MF_2=2\)
\(\Rightarrow S_{MF_1F_2}=\frac{1}{2}MF_1.MF_2=1\)