Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c ,\overrightarrow {OD} = \overrightarrow d \)
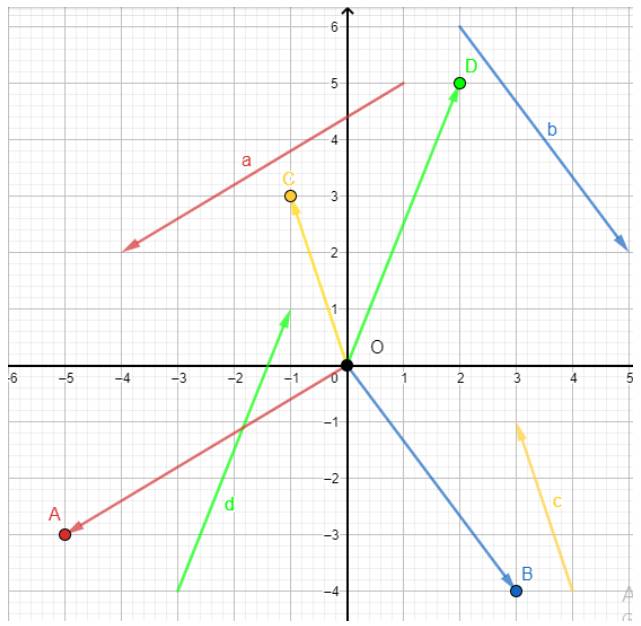
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là:
\(A\left( { - 5; - 3} \right),B\left( {3; - 4} \right),C\left( { - 1;3} \right),D\left( {2;5} \right)\)
Do đó \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right),\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right),\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right),\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\)
b) Vì \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right)\)nên \(\overrightarrow a = \left( { - 5} \right)\overrightarrow i + \left( { - 3} \right)\overrightarrow j = - 5\overrightarrow i - 3\overrightarrow j \)
Vì \(\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right)\) nên \(\overrightarrow b = 3\overrightarrow i + \left( { - 4} \right)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \)
Vì \(\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right)\) nên \(\overrightarrow c = \left( { - 1} \right)\overrightarrow i + \left( 3 \right)\overrightarrow j = - \overrightarrow i + 3\overrightarrow j \)
Vì \(\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\) nên \(\overrightarrow d = 2\overrightarrow i + 5\overrightarrow j \)

(1); vecto u=2*vecto a-vecto b
=>\(\left\{{}\begin{matrix}x=2\cdot1-0=2\\y=2\cdot\left(-4\right)-2=-10\end{matrix}\right.\)
(2): vecto u=-2*vecto a+vecto b
=>\(\left\{{}\begin{matrix}x=-2\cdot\left(-7\right)+4=18\\y=-2\cdot3+1=-5\end{matrix}\right.\)
(3): vecto a=2*vecto u-5*vecto v
\(\Leftrightarrow\left\{{}\begin{matrix}a=2\cdot\left(-5\right)-5\cdot0=-10\\b=2\cdot4-5\cdot\left(-3\right)=15+8=23\end{matrix}\right.\)
(4): vecto OM=(x;y)
2 vecto OA-5 vecto OB=(-18;37)
=>x=-18; y=37
=>x+y=19

Lời giải:
$\overrightarrow{i}=(1,0), \overrightarrow{j}=(0,1)$
$\Rightarrow \overrightarrow{i}-\overrightarrow{j}=(1-0,0-1)=(1,-1)$
Bài 2:
$\overrightarrow{a}+2\overrightarrow{b}=(3+2.-1, -4+2.2)=(1, 0)$

\(\left|\overrightarrow{a}-\overrightarrow{b}\right|=4\)
⇒ \(\left(\overrightarrow{a}-\overrightarrow{b}\right)^2=16\)
⇒ 16 + 9 - 2\(\overrightarrow{a}.\overrightarrow{b}\) = 16
⇒ \(2\overrightarrow{a}.\overrightarrow{b}=9\)
⇒ cosα = \(\dfrac{9}{2.4.3}\)
⇒ cos α = \(\dfrac{3}{8}\)
Vậy chọn D

Giả thiết => cos \(\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{1}{2}\)
⇒ \(\left(\overrightarrow{a};\overrightarrow{b}\right)=60^0\)

a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)