Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

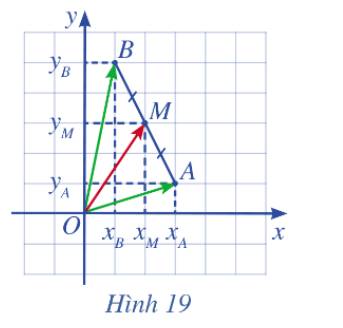
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

a) Vì \(\overrightarrow v = \left( {0; - 7} \right)\)nên \(\overrightarrow v = 0\overrightarrow i + \left( { - 7} \right)\overrightarrow j = - 7\overrightarrow j \)
b) Vì B có tọa độ là (-1; 0) nên \(\overrightarrow {OB} = \left( { - 1;{\rm{ }}0} \right)\). Do đó: \(\overrightarrow {OB} = \left( { - 1} \right)\overrightarrow i + 0\overrightarrow j = - \overrightarrow i \)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

a) Vì \(\overrightarrow a = 3\overrightarrow i \)nên \(\overrightarrow a = \left( {3;0} \right)\)
b) Vì \(\overrightarrow b = - \overrightarrow j \)nên \(\overrightarrow b = \left( {0; - 1} \right)\)
c) Vì \(\overrightarrow c = \overrightarrow i - 4\overrightarrow j \)nên \(\overrightarrow c = \left( {1; - 4} \right)\)
d) Vì \(\overrightarrow d = 0,5\overrightarrow i + \sqrt 6 \overrightarrow j \)nên \(\overrightarrow d = \left( {0,5;\sqrt 6 } \right)\)

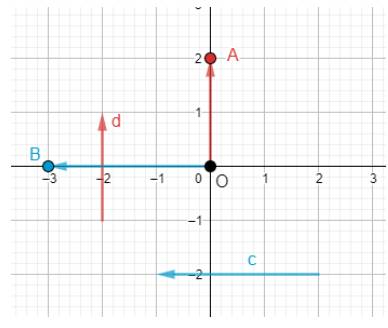
Ta vẽ vecto \(\overrightarrow {OA} = \overrightarrow d \) và \(A\left( {0;2} \right)\). Tọa độ \(\overrightarrow {OA} \) chính là tọa độ của điểm A nên \(\overrightarrow d = \left( {2;2} \right)\)
Ta vẽ vecto \(\overrightarrow {OB} = \overrightarrow c \) và \(A\left( { - 3;0} \right)\). Tọa độ \(\overrightarrow {OB} \) chính là tọa độ của điểm B nên \(\overrightarrow c = \left( { - 3;0} \right)\)

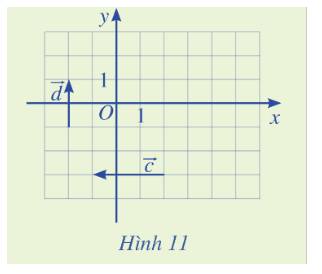
Bước 1: Dựng hình bình hành có cạnh song song với giá của vecto \(\overrightarrow a ,\;\overrightarrow b \) và đường chéo là vecto \(\overrightarrow u ,\;\overrightarrow v \).
Ta dựng được hình hình hành ABCD và DEGH. Trong đó: DC và DE nằm trên giá của vecto \(\overrightarrow a \), DA và DH nằm trên giá của vecto \(\overrightarrow b \), còn vecto \(\overrightarrow u ,\;\overrightarrow v \) lần lượt là hai dường chéo.
Dễ thấy: \(\overrightarrow u = \overrightarrow {DA} + \overrightarrow {DC} ,\;\overrightarrow v = \overrightarrow {DH} + \overrightarrow {DE} \)
Mà \(\overrightarrow {DA} = 3\overrightarrow b ,\;\overrightarrow {DC} = \overrightarrow a \;,\;\overrightarrow {DH} = 3\overrightarrow b ,\;\overrightarrow {DE} = - 2\overrightarrow a .\)
\( \Rightarrow \overrightarrow u = 2\overrightarrow b + \overrightarrow a ,\;\,\overrightarrow v = 3\overrightarrow b - 2\overrightarrow a \)

Lời giải:
$\overrightarrow{i}=(1,0), \overrightarrow{j}=(0,1)$
$\Rightarrow \overrightarrow{i}-\overrightarrow{j}=(1-0,0-1)=(1,-1)$
Bài 2:
$\overrightarrow{a}+2\overrightarrow{b}=(3+2.-1, -4+2.2)=(1, 0)$



a) Vẽ các vecto \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b ,\overrightarrow {OC} = \overrightarrow c ,\overrightarrow {OD} = \overrightarrow d \)
Dựa vào hình vẽ, ta thấy tọa độ của 4 điểm A, B, C, D là:
\(A\left( { - 5; - 3} \right),B\left( {3; - 4} \right),C\left( { - 1;3} \right),D\left( {2;5} \right)\)
Do đó \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right),\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right),\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right),\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\)
b) Vì \(\overrightarrow a = \overrightarrow {OA} = \left( { - 5; - 3} \right)\)nên \(\overrightarrow a = \left( { - 5} \right)\overrightarrow i + \left( { - 3} \right)\overrightarrow j = - 5\overrightarrow i - 3\overrightarrow j \)
Vì \(\overrightarrow b = \overrightarrow {OB} = \left( {3; - 4} \right)\) nên \(\overrightarrow b = 3\overrightarrow i + \left( { - 4} \right)\overrightarrow j = 3\overrightarrow i - 4\overrightarrow j \)
Vì \(\overrightarrow c = \overrightarrow {OC} = \left( { - 1;3} \right)\) nên \(\overrightarrow c = \left( { - 1} \right)\overrightarrow i + \left( 3 \right)\overrightarrow j = - \overrightarrow i + 3\overrightarrow j \)
Vì \(\overrightarrow d = \overrightarrow {OD} = \left( {2;5} \right)\) nên \(\overrightarrow d = 2\overrightarrow i + 5\overrightarrow j \)