Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
\(V=\frac{1}{3}SA.\frac{1}{2}AB.BC=\frac{1}{6}.a.a.2a=\frac{a^3}{3}\)
2.
\(V=\frac{1}{3}SA.S_{ABC}=\frac{1}{3}.2a\sqrt{3}.\frac{a^2\sqrt{3}}{4}=\frac{a^3}{2}\)
P/s: chóp này là chóp "có đáy là tam giác đều" chứ không phải "chóp tam giác đều"
Hai loại này khác xa nhau đấy, ko lộn xộn nhầm lẫn được đâu
3.
Câu này đề sai
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\Rightarrow\Delta SAC\) vuông tại A
\(\Rightarrow SC>SA\) (cạnh huyền luôn lớn hơn cạnh góc vuông)
Do đó đề cho \(SA=SC\) là vô lý
4.
\(AC=BD=\sqrt{AB^2+AD^2}=2a\)
\(\widehat{SCA}=60^0\Rightarrow SA=SC.tan60^0=2a\sqrt{3}\)
\(V=\frac{1}{3}SA.AB.AD=\frac{1}{3}.2a\sqrt{3}.a.a\sqrt{3}=2a^3\)

4.
Gọi M là trung điểm CD, qua M kẻ đường thẳng song song AB
Gọi N là trung điểm AB, qua N kẻ đường thẳng song song AM
Gọi giao của 2 đường thẳng trên là O \(\Rightarrow\) O là tâm (S)
\(\Rightarrow AO=R=\sqrt{3}\)
Đặt \(AB=x;AC=y;AD=z\)
\(AN=\frac{AB}{2}=\frac{x}{2}\) ; \(AM=\frac{CD}{2}=\frac{1}{2}\sqrt{AC^2+AD^2}=\frac{1}{2}\sqrt{y^2+z^2}\)
Áp dụng Pitago: \(AO^2=AN^2+AM^2\)
\(\Rightarrow\frac{x^2}{4}+\frac{1}{4}\left(y^2+z^2\right)=3\Rightarrow x^2+y^2+z^2=12\)
\(V=\frac{1}{3}xyz\le\frac{1}{3}\left(\frac{x+y+z}{3}\right)^3\le\frac{1}{3}\left(\frac{\sqrt{3\left(x^2+y^2+z^2\right)}}{3}\right)^3=\frac{8}{3}\)
2.
Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\frac{1}{2}AC=\frac{a\sqrt{2}}{2}\)
\(SO=\sqrt{SA^2-OA^2}=\frac{a}{2}\)
Áp dụng công thức từ câu 1:
\(R=\frac{SA^2}{2SO}=\frac{3a}{4}\)
3.
\(BC=AB\sqrt{2}=2a\)
Gọi H là hình chiếu của S lên (ABC) \(\Rightarrow\) H đồng thời là tâm đường tròn ngoại tiếp đáy
\(\Rightarrow\) H là trung điểm BC
\(\Rightarrow\widehat{SAH}=60^0\Rightarrow SH=AH.tan60^0=\frac{BC}{2}tan60^0=a\sqrt{3}\)
\(SA=\frac{AH}{cos60^0}=2a\)
\(\Rightarrow R=\frac{SA^2}{2SH}=\frac{2\sqrt{3}a}{3}\)
\(S=4\pi R^2=\frac{16\pi a^2}{3}\)

4.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp AH\)
Mà \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp SC\)
Lại có \(AK\perp SC\)
\(\Rightarrow SC\perp\left(AKH\right)\Rightarrow SK\) là đường cao của chóp S.AHK ứng với đáy là tam giác AHK vuông tại H (do \(AH\perp\left(SBC\right)\Rightarrow AH\perp HK\))
Áp dụng hệ thức lượng:
\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AB^2}=\)
À thôi đến đây phát hiện ra đề bài sai
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AB\Rightarrow\) tam giác SAB vuông tại A với SA là cạnh góc vuông, SB là cạnh huyền
\(\Rightarrow SB>SA\Rightarrow SB=SA=a\) là hoàn toàn vô lý

Câu 5:
Tương tự câu 4, ta thấy tâm $I$ của khối cầu ngoại tiếp $S.ABCD$ là trung điểm $SC$
Theo định lý Pitago:
$SA^2=SB^2-AB^2=(a\sqrt{3})^2-a^2=2a^2$
$AC^2=AB^2+BC^2=a^2+a^2=2a^2$
$SC=\sqrt{SA^2+AC^2}=\sqrt{2a^2+2a^2}=2a$
Do đó: $R=SI=IC=\frac{SC}{2}=a$
Thể tích khối cầu ngoại tiếp S.ABCD là:
$V=\frac{4}{3}\pi R^3=\frac{4}{3}\pi a^3$
Đáp án A
Câu 4:
$AC=\sqrt{AB^2+AD^2}=2a$
$(SC, (ABCD))=\widehat{SCA}=60^0$
$\Rightarrow \frac{SA}{AC}=\tan \widehat{SCA}=\tan 60^0=\sqrt{3}$
$\Rightarrow SA=\sqrt{3}.AC=2\sqrt{3}a$
$SC=\sqrt{SA^2+AC^2}=\sqrt{(2\sqrt{3}a)^2+(2a)^2}=4a$
Gọi $I$ tâm mặt cầu ngoại tiếp hình chóp. $IS=IA=IC$ nên $I$ là tâm ngoại tiếp tam giác $SAC$
$\Rightarrow I$ là trung điểm $SC$.
Bán kính $IS=IC=\frac{AC}{2}=\frac{4a}{2}=2a$
Đáp án A

a) \(A=\left[\left(\frac{1}{5}\right)^2\right]^{\frac{-3}{2}}-\left[2^{-3}\right]^{\frac{-2}{3}}=5^3-2^2=121\)
b) \(B=6^2+\left[\left(\frac{1}{5}\right)^{\frac{3}{4}}\right]^{-4}=6^2+5^3=161\)
c) \(C=\frac{a^{\sqrt{5}+3}.a^{\sqrt{5}\left(\sqrt{5}-1\right)}}{\left(a^{2\sqrt{2}-1}\right)^{2\sqrt{2}+1}}=\frac{a^{\sqrt{5}+3}.a^{5-\sqrt{5}}}{a^{\left(2\sqrt{2}\right)^2-1^2}}\)
\(=\frac{a^{\sqrt{5}+3+5-\sqrt{5}}}{a^{8-1}}=\frac{a^8}{a^7}=a\)
d) \(D=\left(a^{\frac{1}{2}}-b^{\frac{1}{2}}\right)^2:\left(b-2b\sqrt{\frac{b}{a}}+\frac{b^2}{a}\right)\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left[1-2\sqrt{\frac{b}{a}}+\left(\sqrt{\frac{b}{a}}\right)^2\right]\)
\(=\left(\sqrt{a}-\sqrt{b}\right)^2:b\left(1-\sqrt{b}a\right)^2\)

Dễ dàng chứng minh MN // BC
Xét \(\Delta SBC\) có MN // BC và MN đi qua trọng tâm G
\(\Rightarrow\) \(\begin{cases}SM=\frac{2}{3}SB\\SN=\frac{2}{3}SC\end{cases}\)
Sử dụng công thức tỉ lệ thể tích đố với 2 khối tứ diện S.AMN và S.ABC ta có
\(\frac{V_{S.AMN}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SM}{SB}.\frac{SN}{SC}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\\ \Rightarrow V_{S.AMN}=\frac{4}{9}.V_{S.ABC}\)
Tính được \(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{a^3}{6}\)
\(\Rightarrow V_{S.AMN}=\frac{2a^3}{27}\)

Câu 1:
Giải trâu bò: \(m=\frac{x+1}{\sqrt{2x^2+1}}\)
Đặt \(f\left(x\right)=\frac{x+1}{\sqrt{2x^2+1}}\Rightarrow f'\left(x\right)=\frac{\sqrt{2x^2+1}-\frac{\left(x+1\right).2x}{\sqrt{2x^2+1}}}{2x^2+1}=\frac{2x^2+1-2x^2-2x}{\left(2x^2+1\right)\sqrt{2x^2+1}}=\frac{1-2x}{\left(2x^2+1\right)\sqrt{2x^2+1}}\)
\(f'\left(x\right)=0\Rightarrow x=\frac{1}{2}\Rightarrow\) từ BBT ta thấy hàm số đạt cực đại tại \(x=\frac{1}{2}\)
\(\Rightarrow m< f\left(\frac{1}{2}\right)=\frac{\sqrt{6}}{2}\)
Mặt khác ta có:
\(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=\lim\limits_{x\rightarrow+\infty}\frac{x+1}{\sqrt{2x^2+1}}=lim\frac{1+\frac{1}{x}}{\sqrt{2+\frac{1}{x^2}}}=\frac{\sqrt{2}}{2}\)
\(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=\lim\limits_{x\rightarrow-\infty}\frac{x+1}{\sqrt{2x^2+1}}=\lim\limits_{x\rightarrow-\infty}\frac{1+\frac{1}{x}}{-\sqrt{2+\frac{1}{x^2}}}=-\frac{\sqrt{2}}{2}\)
\(\Rightarrow-\frac{\sqrt{2}}{2}< m< \frac{\sqrt{6}}{2}\)
Câu 2:
S A B C G M N P
\(V_{S.ABC}=\frac{1}{6}SA.AB.BC=\frac{1}{6}a^3\)
Qua G kẻ đường thẳng song song BC lần lượt cắt SB, SC tại M và N
Gọi P là trung điểm SC, áp dụng định lý Talet:
\(\frac{PN}{PC}=\frac{PG}{BP}=\frac{1}{3}\Rightarrow\frac{SN}{SC}=\frac{SM}{SB}=\frac{PN+SP}{2SP}=\frac{PN+PC}{2PC}=\frac{2}{3}\)
Áp dụng công thức Simsons:
\(\frac{V_{S.ANM}}{V_{S.ABC}}=\frac{SA}{SA}.\frac{SN}{SC}.\frac{SM}{SB}=1.\frac{2}{3}.\frac{2}{3}=\frac{4}{9}\Rightarrow V_{S.ANM}=\frac{4}{9}V_{SABC}=\frac{2}{27}a^3\)
\(\Rightarrow V_{ABCNM}=V_{SABC}-V_{SANM}=\frac{1}{6}a^3-\frac{2}{27}a^3=\frac{5}{54}a^3\)
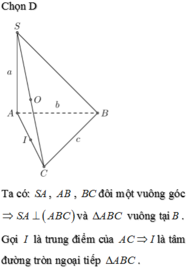

Nếu đề bài hoàn toàn chính xác thì tất cả các đáp án đều sai, tâm mặt cầu sẽ là chính trung điểm của SC nên \(R=\frac{SC}{2}=\frac{c}{2}\)
Còn nếu dữ kiện đề bài là \(SA=a,AB=b,BC=c\) (và các hoán vị của bộ 3 đoạn thẳng này) thì đáp án là \(R=\frac{1}{2}\sqrt{a^2+b^2+c^2}\)