Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

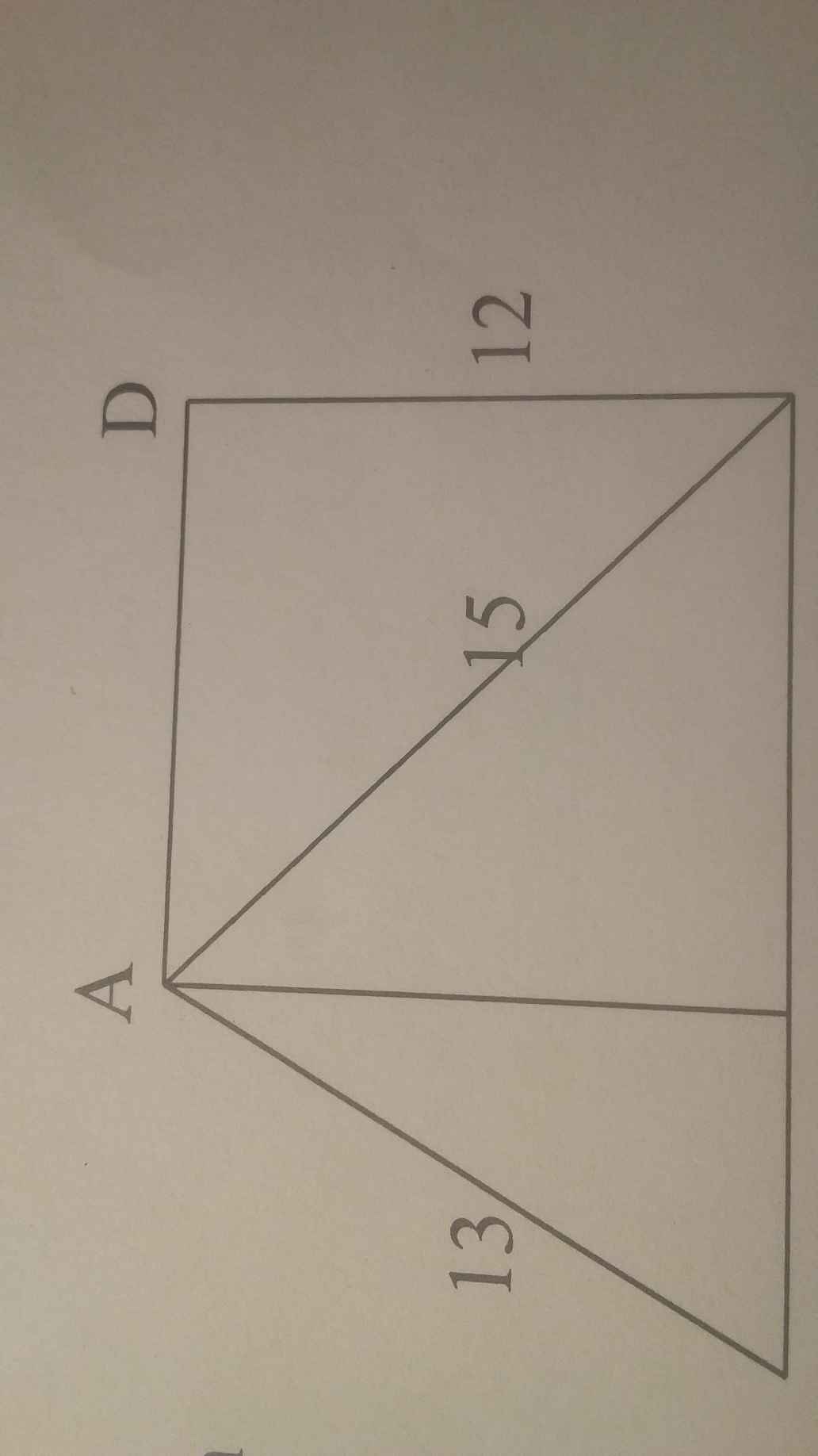
Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)

a: Xét ΔABD và ΔACD có
AB=AC
góc BAD=góc CAD
AD chung
=>ΔABD=ΔACD
=>BD=CD và góc ADB=góc ADC=180/2=90 độ
=>AD vuông góc bC
b: BD=CD=18/2=9cm
AD=căn 15^2-9^2=12cm
c: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I

a: AC=12cm
Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
b: Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
Suy ra: CB=CD

a) AC = ?
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta có:
AC2 = AB2 + BC2
= 52 + 122 = 25 + 144 = 169
⇒ AC = 13 (cm)
b) ΔEAD cân
Xét hai tam giác vuông ABE và DBE có:
AB = BD (gt)
BE là cạnh chung
Do đó: ΔABE = ΔDBE (hai cạnh góc vuông)
⇒ EA = ED (hai cạnh tương ứng)
⇒ ΔEAD cân tại E.
c) K là trung điểm của DC.
Ta có: BE = 4, BC = 12
⇒ BE = 1/3 BC
Hay E là trọng tâm của ΔACD.
⇒ AE là đường trung tuyến ứng với cạnh DC
⇒ K là trung điểm của DC.
d) AD < 4EK
Ta có: EA > AB, ED > BD
Mà AD = AB + BD, AE = ED (câu b)
⇒ 2AE > AD
Và EK = 1/2EA , nhân 2 vế cho 4. Ta được: 4EK = 2EA
Vì 2AE > AD (cmt), 4EK = 2EA ⇒ 4EK > AD (đpcm)

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

Bạn nên ktra lại con số 15cm
a/ Áp dụng định lí Pythagoras cho t/g ABC vuông tại A có
\(AB^2+AC^2=BC^2\)
=> \(AC=\sqrt{161}\) (cm)
b/ t/g ABH vuông tại H và t/g EBH vuông tại H có
AB = EB
BH : chung
=> t/g ABH=t/g EBH (ch-cgv)
=> HA = HE (2 cạnh t/ứ)
c/ Có \(\widehat{BAH}=\widehat{BEH}\) (do t/g ABH = t/g EBH)
=> \(180^o-\widehat{BAH}=180^o-\widehat{BEH}\)
=> \(\widehat{EAD}=\widehat{AEC}\)
=> t/g AEC = t/g EAD
=> AC = DE
d/
AB = BEAD = EC
=> AB + AD = BE + EC
=> BD = BC=> t/g BCD cân tại B
Có t/g ABH = t/g EBH
=> \(\widehat{ABH}=\widehat{EBH}\)
=> BH là pg góc ABEHay BH là pg góc DBCXét t/g BDC có BH là đường pg
=> BH đồng thời là đường cao
=> BH ⊥ DC