NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
2
10 tháng 1 2016
Mỗi góc ngoài của một tam giác bằng tổng của hai góc trong không kề với nó.
24 tháng 11 2021
a. B = 55 độ
C = 35
b. lỗi. phải là 360 độ
ông họ ngô
tôi họ đinh
25 tháng 10 2023
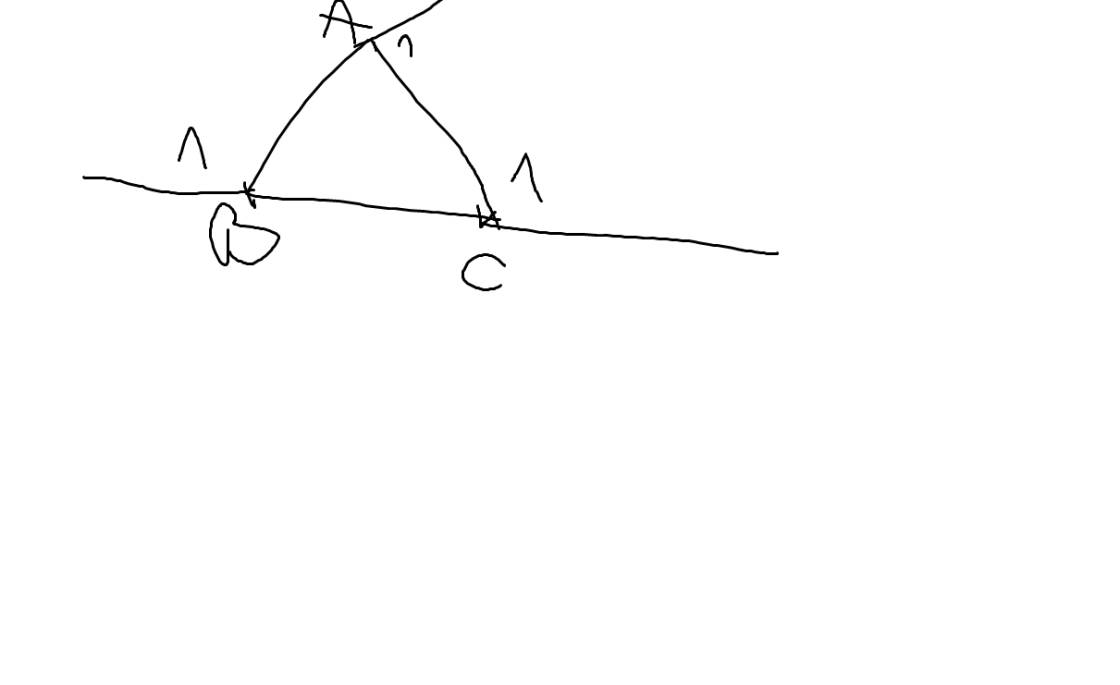
Gọi \(\widehat{A_1};\widehat{B_1};\widehat{C_1}\) lần lượt là các góc ngoài tại các đỉnh A,B,C của ΔABC
Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\widehat{B_1}+\widehat{ABC}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}=180^0-\widehat{ABC}\)
\(\widehat{C_1}+\widehat{ACB}=180^0\)(hai góc kề bù)
=>\(\widehat{C_1}=180^0-\widehat{ACB}\)
\(\widehat{A_1}+\widehat{BAC}=180^0\)(hai góc kề bù)
=>\(\widehat{A_1}=180^0-\widehat{BAC}\)
\(\widehat{A_1}+\widehat{B_1}+\widehat{C_1}\)
\(=180^0-\widehat{BAC}+180^0-\widehat{ABC}+180^0-\widehat{ACB}\)
\(=540^0-180^0=360^0\)
NG
1
AH
Akai Haruma
Giáo viên
22 tháng 11 2021
Lời giải:
Gọi $\widehat{A}, \widehat{B}, \widehat{C}$ là 3 góc trong tam giác $ABC$ và $\widehat{A_1}, \widehat{B_1}, \widehat{C_1}$ tương ứng là 3 góc ngoài 3 đỉnh.
Ta có:
$\widehat{A_1}+\widehat{B_1}+\widehat{C_1}=(180^0-\widehat{A})+(180^0-\widehat{B})+(180^0-\widehat{C})$
$=540^0-(\widehat{A}+\widehat{B}+\widehat{C})$
$=540^0-180^0=360^0$
10 tháng 5 2017
Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)
\(\Rightarrow\widehat{A}=12^o.3=36^o\)
\(\widehat{B}=12^o.5=60^o\)
\(\widehat{C}=12^o.7=84^o\)
QN
16 tháng 7 2017
nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)
vậy : A = 3 . 12 = 36
B = 5 . 12 = 60
C = 7 . 12 = 84
=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)
CT
1
15 tháng 11 2017
Bạn xem ở đường link này:
Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath
NM
Nguyễn Minh Quang
Giáo viên
6 tháng 11 2020
Hình vẽ a chèn không rõ được không, chắc giống của e thôi.
https://1drv.ms/u/s!AhUPZHs4UJtKilHrVZWqF8i6a584?e=0TIfMP
Ta có : \(\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BIC}=180^0-\frac{\widehat{ABC}}{2}-\frac{\widehat{ACB}}{2}\)( Do IB,IC là tia phân giác của góc ABC và ACB)
còn \(\widehat{BKC}=180^0-\widehat{KBC}-\widehat{KCB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BKC}=180^0-\frac{\widehat{xBC}}{2}-\frac{\widehat{yCB}}{2}\)( Do KB,KC là tia phân giác của góc ABC và ACB)
Mà \(\hept{\begin{cases}\widehat{xBC}=180^0-\widehat{ABC}\\\widehat{yCB}=180^0-\widehat{ACB}\end{cases}}\)\(\Rightarrow\widehat{BKC}=180^0-\left(\frac{180^0-\widehat{ABC}}{2}+\frac{180^0-\widehat{ACB}}{2}\right)\)
\(\Rightarrow\widehat{BKC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\)