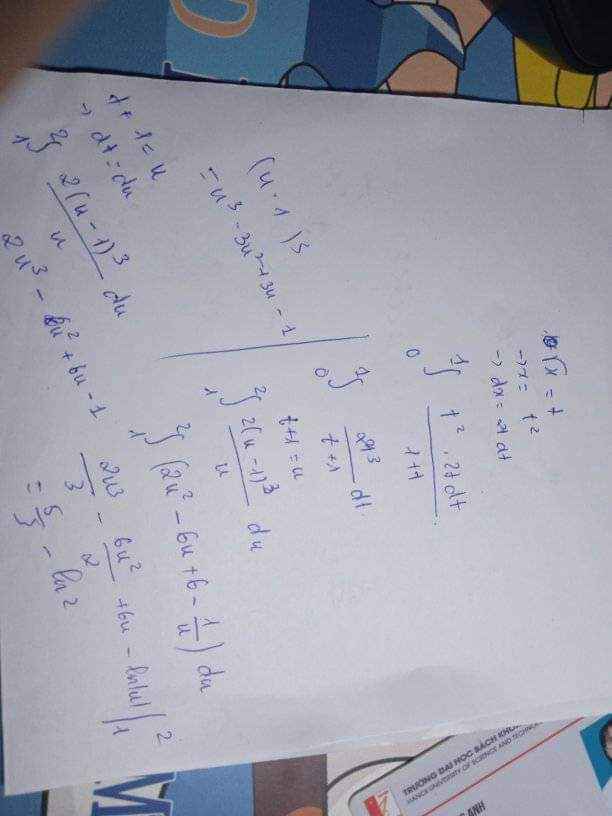Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^{2019}-y^{2019}+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}\right)+2\left(x-y\right)=0\)
<=> \(\left(x-y\right)\left(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2\right)=0\)(1)
Có: \(x^{2018}+x^{2017}y+...+xy^{2017}+y^{2018}+2>0\)mọi x, y.
(1) <=> \(x-y=0\)
<=> x = y
Thế vào P ta có:
\(P=x^4-2x^2+2=\left(x^2-1\right)^2+1\ge1\)
"=" xảy ra <=> \(y=x=\pm1\)
Vậy min P =1 khi và chỉ khi x = y =1 hoặc x = y =-1.

\(I_1=\int\limits^0_{-1}x\left(x^2-4\right)^{2019}dx=\dfrac{1}{2}\int\limits^0_{-1}\left(x^2-4\right)^{2019}d\left(x^2-4\right)\)
\(=\dfrac{1}{4040}\left(x^2-4\right)^{2020}|^0_{-1}=\dfrac{4^{2020}-3^{2020}}{4040}\)
\(I_2=\int\limits^0_{-1}x\left(x-6\right)^{2019}dx\)
Đặt \(x-6=t\Rightarrow dx=dt;\left\{{}\begin{matrix}x=-1\Rightarrow t=-7\\x=0\Rightarrow t=-6\end{matrix}\right.\)
\(\Rightarrow I_2=\int\limits^{-6}_{-7}\left(t+6\right)t^{2019}dt=\int\limits^{-6}_{-7}\left(t^{2020}+6t^{2019}\right)dt\)
\(=\left(\dfrac{t^{2021}}{2021}+\dfrac{3t^{2020}}{1010}\right)|^{-6}_{-7}=\dfrac{7^{2021}-6^{2021}}{2021}-\dfrac{3}{1010}\left(7^{2020}-6^{2020}\right)\)

= -2³/3 + 2²/2 + 2.2 - [-(-1)³/3 + (-1)²/2 + 2.(-1)]
= -8/3 + 2 + 4 - 1/3 - 1/2 + 2
= 8 - 3 - 1/2
= 9/2
\(\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)|^2_{-1}=\dfrac{9}{2}\)

đặt \(x=\frac{\sqrt{3}}{cost};\forall t\in\left(0;\frac{\pi}{2}\right)\Rightarrow tant>0\)
\(dx=d\left(\frac{\sqrt{3}}{cost}\right)=\frac{-\sqrt{3}sint}{cos^2t}dt\)
Thay vào, ta có \(\int\frac{\sqrt{3}\cdot\frac{-\sqrt{3}sint}{cos^2t}}{\frac{\sqrt{3}}{cost}\sqrt{\frac{3}{cos^2t}-3}}dt=\int\frac{-3\cdot\frac{sint}{cos^2t}}{\frac{3}{cost}\cdot\sqrt{tan^2t}}dt=\int\frac{-sint}{cost\cdot tant}dt=-\int dt=-t+C\)
Bây giờ thay t vào là ra

\(I=\int\limits^{\dfrac{\pi}{2}}_0\left(1+cosx+x.cosx\right)e^{sinx}dx=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right).cosx.e^{sinx}dx=I_1+I_2\)
Xét \(I_2\), đặt \(\left\{{}\begin{matrix}u=x+1\\dv=cosx.e^{sinx}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{sinx}\end{matrix}\right.\)
\(\Rightarrow I_2=\left(x+1\right).e^{sinx}|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx=\left(\dfrac{\pi}{2}+1\right)e-1-I_1\)
\(\Rightarrow I=I_1+\left(\dfrac{\pi}{2}+1\right)e-1-I_1=\left(\dfrac{\pi}{2}+1\right)e-1\)

\(I=\int\limits^{\dfrac{\pi}{4}}_0xsinxdx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sinxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cosx\end{matrix}\right.\)
\(\Rightarrow I=-x.cosx|^{\dfrac{\pi}{4}}_0+\int\limits^{\dfrac{\pi}{4}}_0cosxdx=\left(-x.cosx+sinx\right)|^{\dfrac{\pi}{4}}_0=-\dfrac{\pi\sqrt{2}}{8}+\dfrac{\sqrt{2}}{2}\)