K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
1
Y
27 tháng 3 2018
a) \(\frac{x}{-5}>0\)
\(\Rightarrow-5x>0\)
\(\Rightarrow5x< 0\)
\(\Rightarrow x< 0\)
\(\Rightarrow x\in(-1,-2,-3,...)\)
b) \(\frac{2x}{5}=0\)
\(\Rightarrow2x=0\)
\(\Rightarrow x=0\)
c) \(0< \frac{x}{1}< 1\)
\(\Rightarrow0< x< 1\) mà x\(\in z\)
\(\Rightarrow x\in\varnothing\)
d) \(\frac{3x}{6}=1\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=2\)
e) \(2< \frac{x}{3}< 4\)
\(\Rightarrow\)\(6< x< 12\)
\(x\in(7,8,9,10,11,12)\)
PQ
3
AD
26 tháng 12 2020
a) x-3=-3
x=0
b) 7+x=1
x=-6
c) /x/+3=4
/x/=1
=>x=1 hoặc x=-1
d) /x+2/=2
x+2=2 hoặc x+2=-2
x=0 x=-4
e) /x-1/=0
x-1=0
x=1
f) /x-1/=2
x-1=2 hoặc x-1=-2
x=3 x=-1
#Hoctot
BA
9 tháng 2 2016
ta có: \(\frac{84}{14}\)<3x<\(\frac{108}{9}\)
rút gọn cho 3 ta đc : 2<x<4
Vậy x cần tìm là 3
9 tháng 2 2016
Ta có :
84/14<3x<108/9
Rút gọn các số trên ta được: 2<x<4=> x=3
Vậy x=3
(năm mới vui vẻ.........hihihihihihi........t..i..c..k n..h..a..)
6 tháng 2 2021
a) \(15-5\left|x+4\right|=-12-3\)
\(\Leftrightarrow5\left|x+4\right|=30\)
\(\Leftrightarrow\left|x+4\right|=6\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=6\\x+4=-6\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-10\end{cases}}\)
b) \(\left(4x-8\right)\left(7-x\right)=0\Leftrightarrow\orbr{\begin{cases}4x-8=0\\7-x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=7\end{cases}}\)
c) \(\left(x^2-36\right)\left(x^2+5\right)=0\Rightarrow\left(x-6\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\x+6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=-6\end{cases}}\)
d) \(-3\left(x+7\right)-11=2\left(x+5\right)\)
\(\Leftrightarrow-3x-32=2x+10\)
\(\Leftrightarrow5x=-42\Rightarrow x=-\frac{42}{5}\)
29 tháng 12 2018
\(a,x-5⋮x+2\)
\(\Rightarrow x+2-7⋮x+2\)
\(\Rightarrow x+2\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
x + 2 = 1=> x = -1
x + 2 = -1 => x = -3
.... tương tự nhé ~
29 tháng 12 2018
\(2x+3⋮x-5\)
\(\Rightarrow2x-10+7⋮x-5\)
\(\Rightarrow2\left(x-5\right)+7⋮x-5\)
\(\Rightarrow x-5\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
x - 5 = 1 => x = 6
....
31 tháng 7 2020
vì 0<x,y,z\(\le\)1 nên (1-x)(1-y) >=0 <=> 1+xy >= x+y
<=> 1+z+xy >= x+y+z
<=> \(\frac{y}{1+z+xy}\le\frac{y}{x+y+z}\left(1\right)\)
tương tự có \(\frac{x}{1+y+xz}\le\frac{x}{x+y+z}\left(2\right);\frac{z}{1+x+xy}\le\frac{z}{x+y+z}\left(3\right)\)
cộng theo vế của (1), (2), (3) ta được
\(\frac{x}{1+y+xz}+\frac{y}{1+z+xy}+\frac{z}{1+x+yz}\le\frac{x+y+z}{x+y+z}\le\frac{3}{x+y+z}\)
dấu "=" xảy ra khi x=y=z=1
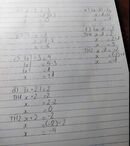
x thuộc các số:{-4;-5;-6;...}