K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 3 2020
\(4n+3⋮n\)
Do \(4n⋮n\) nên để \(4n+3⋮n\) thì \(3⋮n\)
\(\Rightarrow n\inƯ\left(3\right)\)
\(\Rightarrow n\in\left\{1;3;-1;-3\right\}\)
8 tháng 10 2018
\(a,\left(n+5\right)⋮\left(n+2\right)\)
\(\left(n+2+3\right)⋮\left(n+2\right)\)
\(\Rightarrow3⋮\left(n+2\right)\)
\(\Rightarrow n+2\in\left(1;-1;3;-3\right)\)
\(\Rightarrow n\in\left(-1;-3;1;-5\right)\)
b,c,d Tự làm
* Do p > 3 , mà một số > 3 khi chia cho 3 có hai trường hợp xảy ra : 3k + 1 ; 3k + 2.(k thuộc N)(ko lấy 3k vì 3k là hợp số)
Với p = 3k + 1
=> p + 8 = 3k + 1 + 8 = 3k + 9 ko phải là SNT
Với p = 3k + 2
=> p + 8 = 3k + 10 là SNT
=> p + 100 = 3k + 2 + 100 = 3k + 102 là hợp số .
Vậy p + 100 là hợp số
4 tháng 2 2020
a) Ta có : n+2\(⋮\)n-3
\(\Rightarrow\)n-3+5\(⋮\)n-3
Vì n-3\(⋮\)n-3 nên 5\(⋮\)n-3
\(\Rightarrow n-3\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
+) n-3=-1\(\Rightarrow\)n=2 (t/m)
+) n-3=1\(\Rightarrow\)n=4 (t/m)
+) n-3=-5\(\Rightarrow\)n=-2 (t/m)
+) n-3=5\(\Rightarrow\)n=8 (t/m)
Vậy n\(\in\){-2;2;4;8}
HT
1
BT
28 tháng 2 2018
4n-9 = 4n+2-11 = 2(2n+1)-11. Nhận thấy: 2(2n+1) chia hết cho 2n+1 với mọi n
=> Để (4n-9) chia hết cho 2n+1 thì 11 phải chia hết cho 2n+1
=> 2n+1 = (-11,-1,1,11)
| 2n+1 | -11 | -1 | 1 | 11 |
| n | -6 | -1 | 0 | 5 |
NN
0
VD
1
DD
Đoàn Đức Hà
Giáo viên
27 tháng 9 2021
\(4n+9=4n+2+7=2\left(2n+1\right)+7\)chia hết cho \(2n+1\)
tương đương với \(7\div\left(2n+1\right)\)mà \(n\)nguyên nên
\(2n+1\inƯ\left(7\right)=\left\{-7,-1,1,7\right\}\)
\(\Leftrightarrow n\in\left\{-4,-1,0,3\right\}\).
TT
6
HN
4 tháng 1 2019
\(4n-5⋮n-3\Leftrightarrow4n-12+7⋮n-3\)
\(\Leftrightarrow4\left(n-3\right)+7⋮n-3\)
\(\Leftrightarrow7⋮n-3\) ( vì \(n-3\inℤ\) )
\(\Leftrightarrow n-3\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
\(\Leftrightarrow n\in\left\{2;4;-4;10\right\}\)
Vậy n = ...................
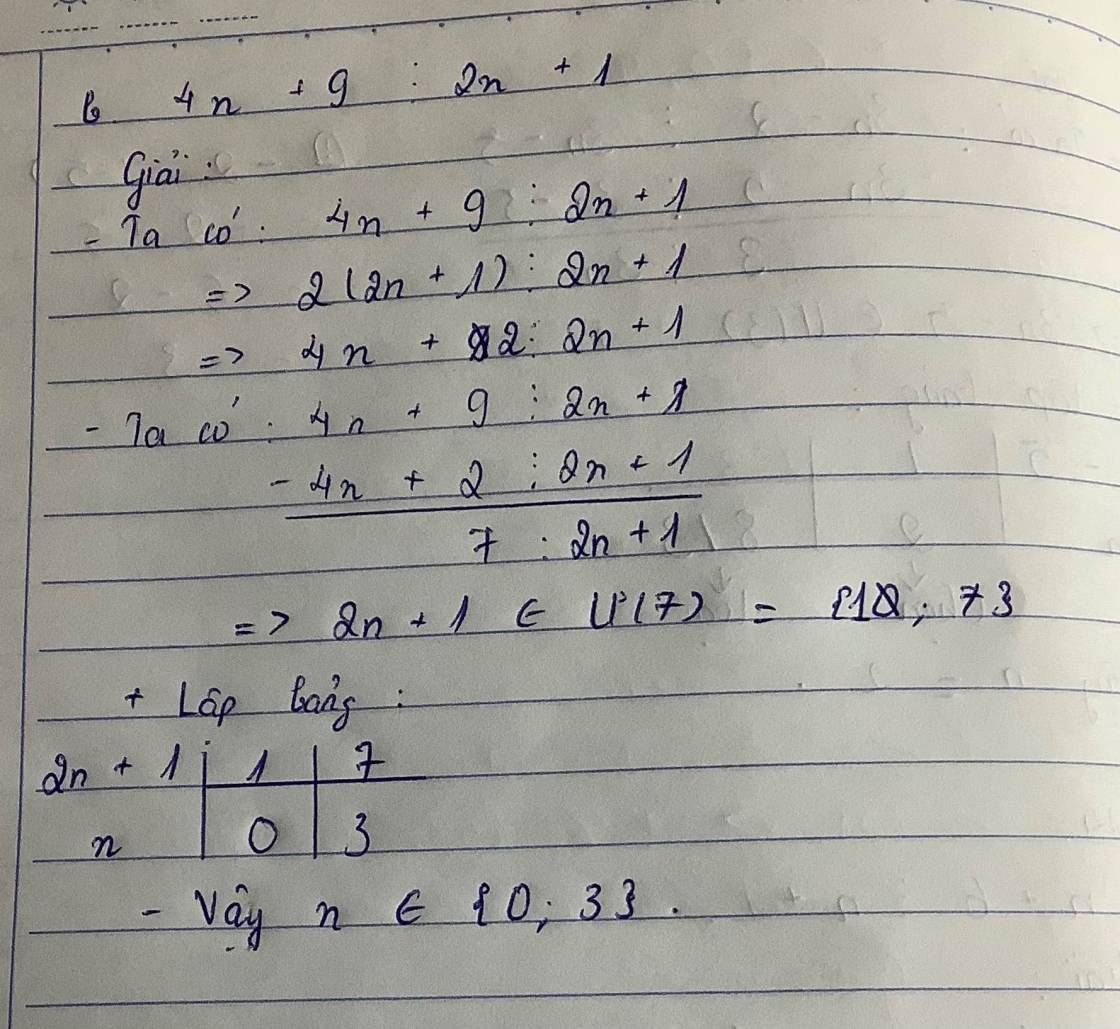
Bạn nào trả lời nhanh mik sẽ k nhé!