K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TL
1
TL
2
23 tháng 7 2016
b.\(\left(x^2+x+1\right)^2\ge0\) vs mọi x
=>\(\left(x^2+x+1\right)^2-\frac{13}{14}\ge-\frac{13}{14}\)
=> bt đạt GTNN =-13/14
c. \(\left(x^2-x+1\right)^2\ge0\) vs mọi x
=> \(\left(x^2-x+1\right)^2+2016\ge2016\)
=> bt đạt GTNN =2016
23 tháng 7 2016
a) 8x-2x^2=-2(x^2-4x)=-2[(x^2-4x+4)-4]=-2(x-2)^2+8 luôn luôn lớn hơn hoặc bằng 8 với mọi x. Dấu bằng xảy ra khi và chỉ khi (x-2)^2=0 <=> x-2=0 <=>x=2
Vậy GTLN là 8 khi và chỉ khi x=2
4 tháng 12 2019
A = x2 + 5y2 + 2x - 4xy - 10y + 14
A = x2 - x2 + x2 + y2 + 4y2 + 2x - 4xy - 10y + 14
A = ( y2 - 10y + 25 ) - ( x2 - 2x + 1 ) + ( x2 - 4xy + 4y2 ) + x2 + 10
A = ( y - 5 )2 - ( x - 1 )2 + ( x - 2y )2 + x2 + 10 \(\ge\)10
Dấu " = " xảy ra \(\Leftrightarrow\)y - 5 = 0 và x - 1 = 0
\(\Rightarrow\)y = 5 và x = 1
Min A = 10 \(\Leftrightarrow\)y = 5 và x = 1
N
2 tháng 12 2018
1) \(A=\frac{2018x^2-2.2018x+2018^2}{2018x^2}=\frac{\left(x-2018\right)^2+2017x^2}{2018x^2}=\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\)
vì \(\frac{\left(x-2018\right)^2}{2018x^2}\ge0\Rightarrow\frac{\left(x-2018\right)^2}{2018x^2}+\frac{2017}{2018}\ge\frac{2017}{2018}\)
dấu = xảy ra khi x-2018=0
=> x=2018
Vậy Min A=\(\frac{2017}{2017}\)khi x=2018
2) \(B=\frac{3x^2+9x+17}{3x^2+9x+7}=\frac{3x^2+9x+7+10}{3x^2+9x+7}=1+\frac{10}{3x^2+9x+7}=1+\frac{10}{3.x^2+9x+7}\)
\(=1+\frac{10}{3.\left(x^2+9x\right)+7}=1+\frac{10}{3.\left[x^2+\frac{2.x.3}{2}+\left(\frac{3}{2}\right)^2\right]-\frac{9}{4}+7}=1+\frac{10}{3.\left(x+\frac{9}{2}\right)^2+\frac{1}{4}}\)
để B lớn nhất => \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\)nhỏ nhất
mà \(3.\left(x+\frac{3}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}\)vì \(3.\left(x+\frac{3}{2}\right)^2\ge0\)
dấu = xảy ra khi \(x+\frac{3}{2}=0\)
=> x=\(-\frac{3}{2}\)
Vậy maxB=\(41\)khi x=\(-\frac{3}{2}\)
3) \(M=\frac{3x^2+14}{x^2+4}=\frac{3.\left(x^2+4\right)+2}{x^2+4}=3+\frac{2}{x^2+4}\)
để M lớn nhất => x2+4 nhỏ nhất
mà \(x^2+4\ge4\)(vì x2 lớn hơn hoặc bằng 0)
dấu = xảy ra khi x2 =0
=> x=0
Vậy Max M\(=\frac{7}{2}\)khi x=0
ps: bài này khá dài, sai sót bỏ qua =))
S
1
22 tháng 10 2020
A = -x2 - 4x - y2 + 2y
= -( x2 + 4x + 4 ) - ( y2 - 2y + 1 ) + 5
= -( x + 2 )2 - ( y - 1 )2 + 5 ≤ 5 ∀ x, y
Dấu "=" xảy ra khi x = -2 ; y = 1
=> MaxA = 5 <=> x = -2 ; y = 1
B = \(\frac{2020}{x^2+2x+6}\)
Để B đạt GTLN => x2 + 2x + 6 đạt GTNN
Ta có : x2 + 2x + 6 = ( x2 + 2x + 1 ) + 5 = ( x + 1 )2 + 5 ≥ 5 ∀ x
Dấu "=" xảy ra khi x = -1
=> Min( x2 + 2x + 6 ) = 5
=> MaxB = 2020/5 = 404 khi x = -1
C = \(\frac{15}{6x-x^2-14}\)
Để C đạt GTNN => 6x - x2 - 14 đạt GTLN
Ta có : 6x - x2 - 14 = -( x2 - 6x + 9 ) - 5 = -( x - 3 )2 - 5 ≤ -5 ∀ x
Dấu "=" xảy ra khi x = 3
=> Max( 6x - x2 - 14 ) = -5
=> MinC = 15/(-5) = -3 khi x = 3
CZ
0
DT
0
D
1
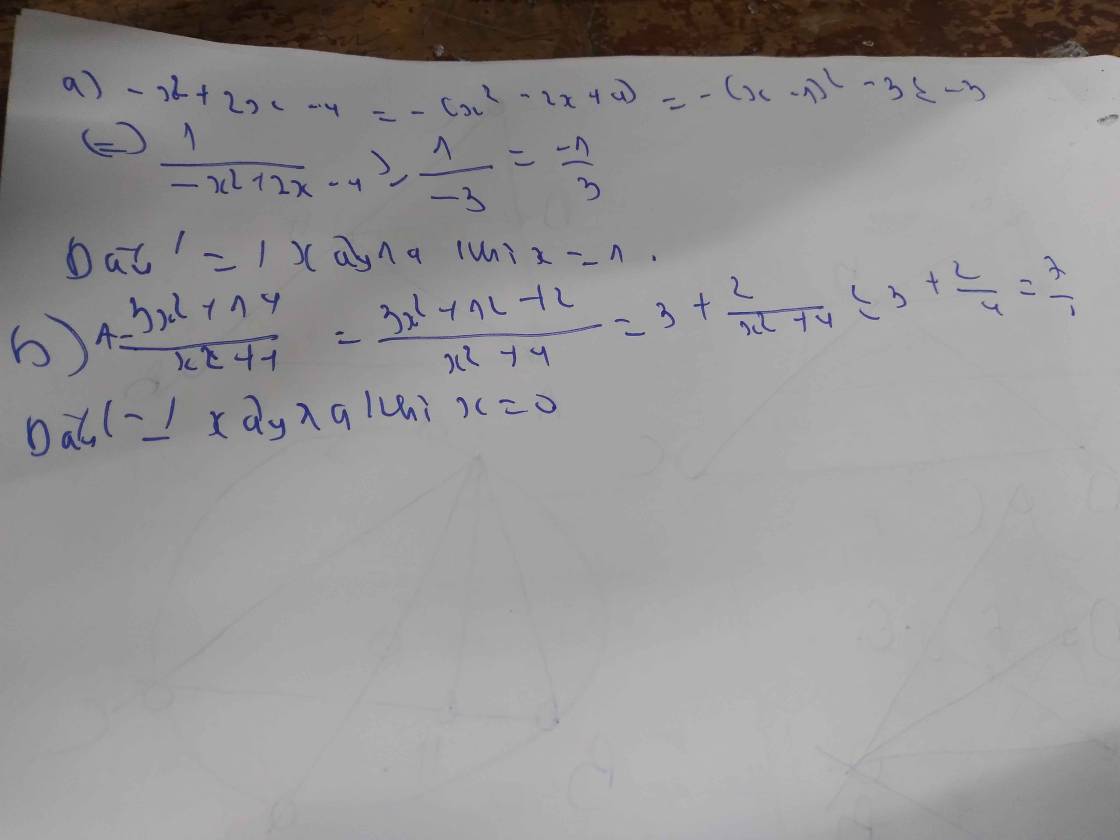
B=2(x^2+2.x.1/4 +1/16)^2 -57/8
=2.(x+1/4)^2 -57/8
MinB=-57/8 khi x=-1/4
\(B=-14+2x^2+x=2\left(x^2+\dfrac{1}{2}x+\dfrac{1}{16}\right)-\dfrac{113}{8}=2\left(x+\dfrac{1}{4}\right)^2-\dfrac{113}{8}\ge-\dfrac{113}{8}\)\(ĐTXR\Leftrightarrow x=-\dfrac{1}{4}\)