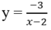Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án: A.
Nhận xét rằng hàm số dạng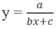 
(a, b ≠ 0) có tiệm cận đứng là 
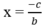và tiệm cận ngang là y = 0.
Đáp án: A.
Nhận xét rằng hàm số dạng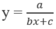 
(a, b
≠
0) có tiệm cận đứng là 
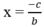và tiệm cận ngang là y = 0.
1.
\(\lim\limits_{x\rightarrow\infty}\frac{3x-2}{x+1}=3\Rightarrow y=3\) là tiệm cận ngang
2.
\(\lim\limits_{x\rightarrow2}\frac{-2x}{x-2}=\infty\Rightarrow x=2\) là tiệm cận đứng
3.
\(\lim\limits_{x\rightarrow\infty}\frac{x-2}{x^2-1}=0\Rightarrow y=0\) là tiệm cận ngang
4.
\(\lim\limits_{x\rightarrow\infty}\frac{x-1}{x^2-x}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow0}\frac{x-1}{x^2-x}=\infty\Rightarrow x=0\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow1}\frac{x-1}{x^2-x}=1\) hữu hạn nên \(x=1\) ko phải tiệm cận đứng
ĐTHS có 2 tiệm cận
a) Vì .png)
và .png)
( hoặc .png)
và .png)
) nên các đường thẳng: x = -3 và x = 3 là các tiệm cận đứng của đồ thị hàm số.
Vì .png)
và .png)
nên các đường thẳng: y = 0 là các tiệm cận ngang của đồ thị hàm số.
b) Hai tiệm cận đứng : .png)
; tiệm cận ngang : .png)
.
c) Tiệm cận đứng : x = -1 ;
vì .png)
nên đồ thị hàm số không có tiệm cận ngang.
d) Hàm số xác định khi : .png)
Vì .png)
( hoặc .png)
) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Vì .png)
nên đường thẳng y = 1 là tiệm cận ngang (về bên phải) của đồ thị hàm số.
1.
Điều kiện xác định của căn thức: \(\left[{}\begin{matrix}x\ge3\\x\le-3\end{matrix}\right.\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{1-1}{1}=0\Rightarrow y=0\) là 1 TCN
\(\lim\limits_{x\rightarrow-\infty}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{-1-1}{-1}=2\Rightarrow y=2\) là 1 TCN
\(\lim\limits_{x\rightarrow-5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}+5}{0}=+\infty\Rightarrow x=-5\) là 1 TCĐ
\(\lim\limits_{x\rightarrow5}\dfrac{\sqrt{x^2+1}-x}{\sqrt{x^2-9}-4}=\dfrac{\sqrt{26}-5}{0}=+\infty\Rightarrow x=5\) là 1 TCĐ
Hàm có 4 tiệm cận
2.
Căn thức của hàm luôn xác định
Ta có:
\(\lim\limits_{x\rightarrow2}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\lim\limits_{x\rightarrow2}\dfrac{\left(2x-1\right)^2-\left(x^2+x+3\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{\left(x-2\right)\left(3x+1\right)}{\left(x-2\right)\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}\)
\(=\lim\limits_{x\rightarrow2}\dfrac{3x+1}{\left(x-3\right)\left(2x-1+\sqrt{x^2+x+3}\right)}=\dfrac{-7}{6}\) hữu hạn
\(\Rightarrow x=2\) ko phải TCĐ
\(\lim\limits_{x\rightarrow3}\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}=\dfrac{5-\sqrt{15}}{0}=+\infty\)
\(\Rightarrow x=3\) là tiệm cận đứng duy nhất
\(\lim\limits_{x\rightarrow-1^+}\dfrac{2x-1}{x+1}=-\infty\Rightarrow x=-1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow+\infty}\dfrac{2x-1}{x+1}=2\Rightarrow y=2\) là tiệm cận ngang
\(\Rightarrow P=3.\left(-1\right)^2-2=1\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ