Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: BC=căn 6^2+8^2=10cm
3:
a: 5cm; 12cm; 9cm
5+12>9; 5+9>12; 12+9>5
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
b: 12+16>20; 12+20>16; 20+16>12
=>Bộ ba số này thỏa mãn độ dài 3 cạnh của 1 tam giác
4:
Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
10:
a: AB=căn 10^2-6^2=8cm
b: Xét ΔMAC và ΔMDB có
MA=MD
góc AMC=góc DMB
MC=MB
=>ΔMAC=ΔMDB
c: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hbh
=>AB//CD

a) +Xét tam giác ABD :
ta có góc B = 60* ,góc BAD = 60*
mà góc B + góc BAD + ADB = 180* ( tổng 3 góc )
=> góc ADB = 60*
=> tam giac ABD là tam giác đều ( mỗi góc = 60*) => AB = BD = AD = 7cm
ta có H là trung diem BD => AH là duong trung tuyến,là tia phan giac goc BAD,là duong cao cùa tam giac ABD ( tam giac ABD đều ) => HD = HB = 1/2 BD = 3.5cm
+áp dụng định lí pitago vào tam giác ABH vuong tai H có AB = 7cm,BH = 3.5 cm :
AB^2 = AH^2 + BH^2 => em tự tính AH nhé
+ta có BH + HC = BC => HC = BC - HB = 15 - 3.5 = 11.5cm
+áp dụng dinh li pitago vào tam giac vuong AHC vuong tai H có AH ( lúc nãy tính ) và HC = 11.5cm
AC^2 =AH^2 + HC^2 => AC =13cm
b) AB ^2 + AC^2 có = BC ^2 ko? nếu = thì tam giac ABC vuong tai A

a) +Xét tam giác ABD :
ta có góc B = 60* ,góc BAD = 60*
mà góc B + góc BAD + ADB = 180* ( tổng 3 góc )
=> góc ADB = 60*
=> tam giac ABD là tam giác đều ( mỗi góc = 60*) => AB = BD = AD = 7cm
ta có H là trung diem BD => AH là duong trung tuyến,là tia phan giac goc BAD,là duong cao cùa tam giac ABD ( tam giac ABD đều ) => HD = HB = 1/2 BD = 3.5cm
+áp dụng định lí pitago vào tam giác ABH vuong tai H có AB = 7cm,BH = 3.5 cm :
AB^2 = AH^2 + BH^2 => em tự tính AH nhé
+ta có BH + HC = BC => HC = BC - HB = 15 - 3.5 = 11.5cm
+áp dụng dinh li pitago vào tam giac vuong AHC vuong tai H có AH ( lúc nãy tính ) và HC = 11.5cm
AC^2 =AH^2 + HC^2 => tự tính AC
b) bạn tính AB ^2 + AC^2 có = BC ^2 ko? nếu = thì tam giac ABC vuong tai A

Bạn vẽ hình nha
Xét tam giác AHB vuông tại h
\(BH=\sqrt{BA^2-AH^2}\)(Py ta go)
\(\Rightarrow BH=\sqrt{10^2-8^2}=6\)
Xét tam giác AHC vuông tại H
\(CH=\sqrt{AC^2-AH^2}\)
\(\Rightarrow CH=15\)
\(\Rightarrow BC=21\Rightarrow BC^2=441\)
Xét \(AB^2+AC^2=10^2+17^2=389\)
\(\Rightarrow BC^2\ne AB^2+AC^2\)
Vậy tam giác ABC không là tam giác vuông

trả lời
Hai cạnh góc vuông của một tam giác vuông có độ dài lần lượt bằng 3cm và 4cm.
Độ dài cạnh huyền của tam giác đó bằng.....5 cm....... cm.
hc tốt

Bạn Chi nói đúng vì ta thấy tỉ số của 2 cạnh góc vuông và cạnh huyền là3,4,5 mà ở đây là 3,5,7.Do đó tam giác ABC không phải là tam giác vuông
Ta có: \(BC^2=7^2=49\)
\(AB^2+AC^2=3^2+5^2=34\)
Vì \(BC^2>AC^2+AB^2\) nên ΔABC không vuông
Vậy: Bạn Chi nói đúng

Gọi các cạnh tương ứng với các đường cao 3 cm; 4cm; 6 cm là a, b, c ( >0; cm )
Ta có: Diện tích của tam giác là:
\(\frac{1}{2}.3.a=\frac{1}{2}.4.b=\frac{1}{2}.6.c\)
=> \(3a=4b=6c\)
=> \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}\)
Độ dài đường cao tỉ lệ nghịch với độ dài cạnh đáy tương ứng => a là cạnh dài nhất
=> b + c - a = 1
Áp dụng dãy tỉ số bằng nhau ta có: \(\frac{a}{\frac{1}{3}}=\frac{b}{\frac{1}{4}}=\frac{c}{\frac{1}{6}}=\frac{b+c-a}{\frac{1}{6}+\frac{1}{4}-\frac{1}{3}}=\frac{1}{\frac{1}{12}}=12\)
=> a = \(\frac{1}{3}.12=4\)cm
b = 3 cm
c = 2 cm
=> Chu vi tam giác là: a + b + c = 4 + 3 + 2 = 9 cm

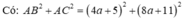

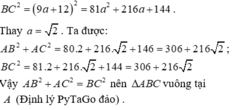
Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A